题目内容
若方程
-
+
=0有增根，则它的增根是（ ）
| 4 |
| x2+2x |
| m |
| x+2 |
| 2 |
| x |
| A、0 | B、-2 | C、1 | D、-2或0 |
分析：根据增根是使分式方程的最简公分母等于0的未知数的值列式求解即可．
解答：解：方程两边都乘以x2+2x得，
4-mx+2（x+2）=0，
∵方程有增根，
∴最简公分母x2+2x=0，
解得x=-2或x=0．
当m=-2时，4-2m+2（-2+2）=0，
解得m=2，
当x=0时，4-0+2（0+2）=8≠0，
所以求不出m的值，方程不存在，
所以x=0不成立，
因此，x=-2．
故选B．
4-mx+2（x+2）=0，
∵方程有增根，
∴最简公分母x2+2x=0，
解得x=-2或x=0．
当m=-2时，4-2m+2（-2+2）=0，
解得m=2，
当x=0时，4-0+2（0+2）=8≠0，
所以求不出m的值，方程不存在，
所以x=0不成立，
因此，x=-2．
故选B．
点评：本题主要考查了分式方程的增根的定义，增根就是使分式方程的最简公分母为0的未知数的值，要注意对所求的x的值进行检验．
练习册系列答案
相关题目
若解方程
-
=
出现增根，则增根为（ ）
| 4 |
| x2-2x |
| x |
| x-2 |
| 2 |
| x |
| A、0或2 | B、0 | C、2 | D、1 |
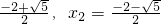，则二次三项式4x2+8x-1可分解因式为
）（
）
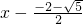）（x+
）
）
）（2x+2+