题目内容
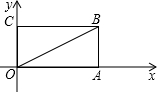以矩形OABC的顶点O为原点，分别以边OA、边OC所在的直线为坐标轴，建立如图所示的直角坐标系，如果AO=4，OC=3，那么对角线OB对应的函数关系式为________．
y=
x
分析：根据已知得出B点的坐标为：（4，3），再利用对角线OB对应的函数关系式为：y=kx，求出即可．
解答：∵以矩形OABC的顶点O为原点，分别以边OA、边OC所在的直线为坐标轴，建立如图所示的直角坐标系，AO=4，OC=3，
∴B点的坐标为：（4，3），
∴假设对角线OB对应的函数关系式为：y=kx，
∴3=4k，
∴k=，
∴y=x，
故答案为：y=x．
点评：此题主要考查了待定系数法求正比例函数解析式，根据题意得出B点的坐标是解决问题的关键．
x分析：根据已知得出B点的坐标为：（4，3），再利用对角线OB对应的函数关系式为：y=kx，求出即可．
解答：∵以矩形OABC的顶点O为原点，分别以边OA、边OC所在的直线为坐标轴，建立如图所示的直角坐标系，AO=4，OC=3，
∴B点的坐标为：（4，3），
∴假设对角线OB对应的函数关系式为：y=kx，
∴3=4k，
∴k=
，∴y=
x，故答案为：y=
x．点评：此题主要考查了待定系数法求正比例函数解析式，根据题意得出B点的坐标是解决问题的关键．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
A点运动，E为AB上一动点，点E以1cm/s的速度从A点出发向点B运动．
10、如图，以矩形OABC的顶点O为原点，OA所在的直线为x轴，OC所在的直线为y轴，建立平面直角坐标系、已知OA=3，OC=2，点E是AB的中点，在OA上取一点D，将△BDA沿BD翻折，使点A落在BC边上的点F处，若在y轴上存在点P，且满足FE=FP，则P点坐标为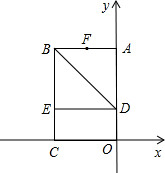
直角坐标系．已知OA=6，OC=4，在OA上取一点D，将△BDA沿BD翻折，点A恰好落在BC边上的点E处．
如图，以矩形OABC的顶点O为原点，OA所在的直线为x轴，OC所在的直线为y轴，建立平面直角坐标系．已知OA=3，OC=2，点E是AB的中点．在OA上取一点D，将△BDA沿BD翻折，使点A落在BC边上的点F处．直接写出点E的坐标