题目内容
如图，以矩形OABC的顶点O为原点，OA所在的直线为x轴，OC所在的直线为y轴，建立平面直角坐标系．已知OA=3，OC=2，点E是AB的中点．在OA上取一点D，将△BDA沿BD翻折，使点A落在BC边上的点F处．直接写出点E的坐标（3，1）
（3，1）
，F坐标是（1，2）
（1，2）
．分析：首先根据矩形的性质可得AB=CO=2，再根据E为中点可得AE的长，再结合OA=3，可得E点坐标；根据折叠可得DA=FD=CO，进而得到DF和DA的长，然后即可算出DO的长，进而得到F点坐标．
解答：解：∵OC=2，四边形OABC是矩形，
∴AB=OC=2，
∵点E是AB的中点，
∴AE=1，
∵AO=3，
∴E（3，1），
根据折叠可得DA=DF，
∴DF=CO=2，
∴AD=2，
∴DO=3-2=1，
∴F（1，2），
故答案为：（3，1）；（1，2）．
∴AB=OC=2，
∵点E是AB的中点，
∴AE=1，
∵AO=3，
∴E（3，1），
根据折叠可得DA=DF，
∴DF=CO=2，
∴AD=2，
∴DO=3-2=1，
∴F（1，2），
故答案为：（3，1）；（1，2）．
点评：此题主要考查了图形的翻折变换，关键是理清翻折以后哪些线段是对应相等的．
练习册系列答案
相关题目
A点运动，E为AB上一动点，点E以1cm/s的速度从A点出发向点B运动．
10、如图，以矩形OABC的顶点O为原点，OA所在的直线为x轴，OC所在的直线为y轴，建立平面直角坐标系、已知OA=3，OC=2，点E是AB的中点，在OA上取一点D，将△BDA沿BD翻折，使点A落在BC边上的点F处，若在y轴上存在点P，且满足FE=FP，则P点坐标为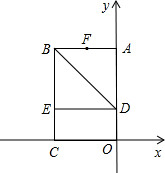
直角坐标系．已知OA=6，OC=4，在OA上取一点D，将△BDA沿BD翻折，点A恰好落在BC边上的点E处．
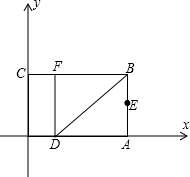系．已知OA=3，OC=2，点E是AB的中点，在OA上取一点D，将△BDA沿BD翻折，使点A落在BC边上的点F处．
如图，以矩形OABC的顶点O为原点，OA所在的直线为x轴，OC所在的直线为y轴，建立平面直角坐标系．已知OA=3，OC=2，点E是AB的中点，在OA上取一点D，将△BDA沿BD翻折，使点A落在BC边上的点F处．