题目内容
如图，⊙Ol和⊙O2内切于点P，⊙O2的弦AB经过⊙Ol的圆心Ol，交⊙Ol于C、D，若AC：CD：DB=3：4：2，则⊙Ol与⊙O2的直径之比为（ ）
A．2：7
B．2：5
C．2：3
D．1：3
【答案】分析：要求直径之比，连接PO2并延长交大圆于M，设AC=3r，CD=4r，DB=2r，由PO1=2r，BOl•AOl=PO1•MOl，
可得MO1=10r，则直径MP=12r，所以可得结论为1：3．
解答：
解：如图示，连接O1O2并延长交大圆于A，且过P点，
∵AC：CD：DB=3：4：2，
∴设AC=3r，CD=4r，DB=2r，
∴PO1=2r，
在⊙O2中由BOl•AOl=PO1•MOl，
即4r•5r=2r•MO1．
∴MO1=10r，
∴直径之比=4r：12r=1：3
点评：这道题考查了相切圆的性质和垂径定理，以及等效代换的应用，同学们应该熟练掌握．
可得MO1=10r，则直径MP=12r，所以可得结论为1：3．
解答：
解：如图示，连接O1O2并延长交大圆于A，且过P点，∵AC：CD：DB=3：4：2，
∴设AC=3r，CD=4r，DB=2r，
∴PO1=2r，
在⊙O2中由BOl•AOl=PO1•MOl，
即4r•5r=2r•MO1．
∴MO1=10r，
∴直径之比=4r：12r=1：3
点评：这道题考查了相切圆的性质和垂径定理，以及等效代换的应用，同学们应该熟练掌握．
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
11、如图，⊙Ol和⊙O2外切于A，PA是内公切线，BC是外公切线，B、C是切点．①PB=AB；②∠PBA=∠PAB；③△PAB∽△OlAB；④PB•PC=OlA•O2A．上述结论，正确结论的个数是（B ）
13、如图，⊙Ol和⊙O2内切于点P，⊙O2的弦AB经过⊙Ol的圆心Ol，交⊙Ol于C、D，若AC：CD：DB=3：4：2，则⊙Ol与⊙O2的直径之比为（ ）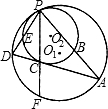
如图，⊙Ol和⊙O2内切于点P，过点P的直线交⊙Ol于点D，交⊙O2于点E，DA与⊙O2相切，切点为C．