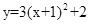题目内容
已知
是抛物线
上的点，则（ ）
A． | B． | C． | D． |
C．
解析试题分析：∵
0，∴抛物线开口向下.
∵抛物线的对称轴为直线
，
∴点
离对称轴最远，点
在对称轴上. ∴.
故选C．
考点：二次函数图象上点的坐标特征．
练习册系列答案
阅读快车系列答案
相关题目
将抛物线y=（x﹣1）2+3向左平移1个单位，再向下平移3个单位后所得抛物线的解析式为（ ）
| A．y=（x﹣2）2 | B．y=（x﹣2）2+6 | C．y=x2+6 | D．y=x2 |
将二次函数y=x2的图象向右平移一个单位长度，再向上平移3个单位长度所得的图象解析式为（ ）
| A．y=（x﹣1）2+3 | B．y=（x+1）2+3 |
| C．y=（x﹣1）2﹣3 | D．y=（x+1）2﹣3 |
抛物线y=-x2可由抛物线y=-(x-2)2+3如何平移得到（ ）
| A．先向左平移2个单位，再向下平移3个单位 |
| B．先向右平移2个单位，再向下平移3个单位 |
| C．先向左平移2个单位，再向上平移3个单位 |
| D．先向右平移2个单位，再向上平移3个单位 |
先向左平移1个单位，再向上平移2个单位，那么所得的新抛物线的解析式是（ ）
抛物线
与x轴的交点坐标是（ ）
| A．（1，0）（-3，0） | B．（-1，0）（3，0） |
| C．（1，0）（3，0） | D．（-1，0）（-3，0） |
二次函数y=ax2+bx+c的图象如图所示，有下列结论：
①a<0，②b<0，③c<0，④4a-2b+c<0，⑤b+2a=0
其中正确的个数有（ ）
| A．1个 | B．2个 | C．3个 | D．4个 |
将二次函数
的图象向右平移2个单位后，所得图象的函数表达式是（ ）
A． | B． | C． | D． |
二次函数y=ax2+bx+c（a、b、c为常数且a≠0）中的x与y的部分对应值如下表：
| x | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 |
| y | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | 12 |
（1）二次函数y=ax2+bx+c有最小值，最小值为﹣3；
（2）当
时，y＜0；（3）二次函数y=ax2+bx+c的图象与x轴有两个交点，且它们分别在y轴两侧．
则其中正确结论的个数是（ ）
A.3 B.2 C.1 D.0