题目内容
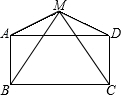 已知:如图,M是矩形ABCD外一点,连接MB、MC、MA、MD,且MA=MD.
已知:如图,M是矩形ABCD外一点,连接MB、MC、MA、MD,且MA=MD.求证:MB=MC.
分析:因为在矩形ABCD中,得到AB=CD,∠BAD=∠CDA=90°.从而得到∠MAD=∠MDA,所以△ABM≌△DCM.而解得.
解答:证明:因为在矩形ABCD中,
所以AB=CD,∠BAD=∠CDA=90°.
因为△AMD中,AM=DM,
所以∠MAD=∠MDA,
所以∠MAB=∠MDC.在△ABM和△DCM中
,
所以△ABM≌△DCM.
所以MB=MC.
所以AB=CD,∠BAD=∠CDA=90°.
因为△AMD中,AM=DM,
所以∠MAD=∠MDA,
所以∠MAB=∠MDC.在△ABM和△DCM中
|
所以△ABM≌△DCM.
所以MB=MC.
点评:本题考查了矩形的性质,考查一是矩形对角线的交点恰好就是等腰三角形底边的中点,二是等腰三角形底边上的中线恰好就是顶角的平分线,正是这两个“巧妙”,为我们作角的平分线提供了一种新方法.

练习册系列答案
相关题目
 27、已知:如图,O是矩形ABCD的对角线的交点,BE∥AC,CE∥BD,试说明OE与CB互相垂直平分.
27、已知:如图,O是矩形ABCD的对角线的交点,BE∥AC,CE∥BD,试说明OE与CB互相垂直平分.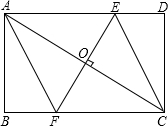 已知:如图,EF是矩形ABCD的对角线AC的垂直平分线,EF与对角线AC及边AD、BC分别交于点O、E、F.
已知:如图,EF是矩形ABCD的对角线AC的垂直平分线,EF与对角线AC及边AD、BC分别交于点O、E、F.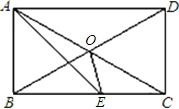 已知:如图,O是矩形ABCD对角线的交点,AE平分∠BAD,∠AOD=120°,∠AEO=
已知:如图,O是矩形ABCD对角线的交点,AE平分∠BAD,∠AOD=120°,∠AEO= 已知:如图,P是矩形ABCD的CD边上一点,PE⊥AC于E,PF⊥BD于F,AC=15,BC=8,求PE+PF.
已知:如图,P是矩形ABCD的CD边上一点,PE⊥AC于E,PF⊥BD于F,AC=15,BC=8,求PE+PF.