题目内容
 已知:如图,P是矩形ABCD的CD边上一点,PE⊥AC于E,PF⊥BD于F,AC=15,BC=8,求PE+PF.
已知:如图,P是矩形ABCD的CD边上一点,PE⊥AC于E,PF⊥BD于F,AC=15,BC=8,求PE+PF.分析:由四边形ABCD为矩形,得到对边相等,对角线互相平分且相等,由OD=OC,利用等边对等角设∠BDC=∠DCA=α,在直角三角形PCE中,利用正弦函数的定义表示出PE,在直角三角形PDF中,利用正弦函数的定义表示出PF,代入PE+PF中提取公因式,且由PD+PC=CD化简,在直角三角形BCD中,由BD与BC的长,利用勾股定理求出CD的长,在直角三角形BCD中,利用正弦函数定义,及BD于BC的长,求出sinα的值,由DC与sinα的值即可求出PE+PF的值.
解答: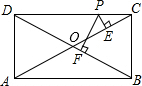 解:∵四边形ABCD是矩形,
解:∵四边形ABCD是矩形,
∴BD=AC=15,OD=OC,
∴设∠BDC=∠DCA=α,
在Rt△PCE中,sin∠DCA=sinα=
,
∴PE=PCsinα,
在Rt△PDF中,sin∠BDC=sinα=
,
∴PF=PDsinα,
∴PE+PF=PCsinα+PDsinα=CDsinα,
∵在Rt△BCD中,BD=15,BC=8,
∴sinα=
,CD=
=
,
∴PE+PF=
×
=
.
 解:∵四边形ABCD是矩形,
解:∵四边形ABCD是矩形,∴BD=AC=15,OD=OC,
∴设∠BDC=∠DCA=α,
在Rt△PCE中,sin∠DCA=sinα=
| PE |
| PC |
∴PE=PCsinα,
在Rt△PDF中,sin∠BDC=sinα=
| PF |
| DP |
∴PF=PDsinα,
∴PE+PF=PCsinα+PDsinα=CDsinα,
∵在Rt△BCD中,BD=15,BC=8,
∴sinα=
| 8 |
| 15 |
| BD2-BC2 |
| 161 |
∴PE+PF=
| 161 |
| 8 |
| 15 |
8
| ||
| 15 |
点评:此题考查了解直角三角形的题型,涉及的知识有:勾股定理,锐角三角函数定义,以及矩形的性质,熟练掌握定理及性质是解本题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 27、已知:如图,O是矩形ABCD的对角线的交点,BE∥AC,CE∥BD,试说明OE与CB互相垂直平分.
27、已知:如图,O是矩形ABCD的对角线的交点,BE∥AC,CE∥BD,试说明OE与CB互相垂直平分.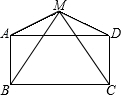 已知:如图,M是矩形ABCD外一点,连接MB、MC、MA、MD,且MA=MD.
已知:如图,M是矩形ABCD外一点,连接MB、MC、MA、MD,且MA=MD.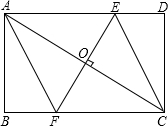 已知:如图,EF是矩形ABCD的对角线AC的垂直平分线,EF与对角线AC及边AD、BC分别交于点O、E、F.
已知:如图,EF是矩形ABCD的对角线AC的垂直平分线,EF与对角线AC及边AD、BC分别交于点O、E、F.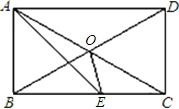 已知:如图,O是矩形ABCD对角线的交点,AE平分∠BAD,∠AOD=120°,∠AEO=
已知:如图,O是矩形ABCD对角线的交点,AE平分∠BAD,∠AOD=120°,∠AEO=