题目内容
已知直线y=
x+m与y轴和x轴分别相交于A，B两点，作OC⊥AB于C．
（1）写出A，B两点的坐标（用含m的代数式表示），并求tanA的值；
（2）如果AC=4
，求m的值．
| 1 |
| 2 |
（1）写出A，B两点的坐标（用含m的代数式表示），并求tanA的值；
（2）如果AC=4
| 5 |
（1）当x=0时，y=m，∴A（0，m）；
当y=0时x=-2m，∴B（-2m，0）．
tanA=
=
=2．
（2）在Rt△ABO中，OA=m，OB=2m，
∴AB=
m，
∵△ACO∽△AOB，
∴OA2=AC•AB，
m2=4
×
m，
∴m1=20，m2=0（不符合题意，舍去）．
∴m的值为20．
当y=0时x=-2m，∴B（-2m，0）．
tanA=
| OB |
| OA |
| 2m |
| m |
（2）在Rt△ABO中，OA=m，OB=2m，
∴AB=
| 5 |
∵△ACO∽△AOB，
∴OA2=AC•AB，
m2=4
| 5 |
| 5 |
∴m1=20，m2=0（不符合题意，舍去）．
∴m的值为20．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
已知直线
E两点，与x轴交于B、C两点，且B点坐标为（1，0）．
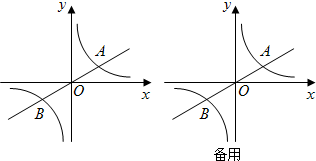
（2013•梧州模拟）如图，已知直线y=