题目内容
如图所示,正方形ABCD的边长为6,M在DC上,且DM=4,N是AC上的动点,则DN+MN的最小值是 .
【答案】分析:连BD,BM,BM交AC于N′,根据正方形的性质得到B点与D点关于AC对称,则有N′D+N′M=BM,利用两点之间线段最短得到BM为DN+MN的最小值,然后根据勾股定理计算即可.
解答: 解:连BD,BM,BM交AC于N′,如图,
解:连BD,BM,BM交AC于N′,如图,
∵四边形ABCD为正方形,
∴B点与D点关于AC对称,
∴N′D=N′B,
∴N′D+N′M=BM,
∴当N点运动到N′时,它到D点与M点的距离之和最小,最小距离等于MB的长,
而BC=CD=6,DM=4,
∴MC=2,
∴BM= =2
=2 .
.
故答案为:2 .
.
点评:此题考查了轴对称-最短路线问题:通过轴对称,把两条线段转化为一条线段,利用两点之间线段最短得到最短路线,然后根据勾股定理进行计算.也考查了正方形的性质.
解答:
 解:连BD,BM,BM交AC于N′,如图,
解:连BD,BM,BM交AC于N′,如图,∵四边形ABCD为正方形,
∴B点与D点关于AC对称,
∴N′D=N′B,
∴N′D+N′M=BM,
∴当N点运动到N′时,它到D点与M点的距离之和最小,最小距离等于MB的长,
而BC=CD=6,DM=4,
∴MC=2,
∴BM=
 =2
=2 .
.故答案为:2
 .
.点评:此题考查了轴对称-最短路线问题:通过轴对称,把两条线段转化为一条线段,利用两点之间线段最短得到最短路线,然后根据勾股定理进行计算.也考查了正方形的性质.

练习册系列答案
相关题目
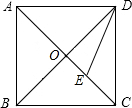 如图所示,正方形ABCD的对角线AC,BD相交于点O,DE平分∠ODC交OC于点E,若AB=2,则线段OE的长为( )
如图所示,正方形ABCD的对角线AC,BD相交于点O,DE平分∠ODC交OC于点E,若AB=2,则线段OE的长为( )A、
| ||||
B、
| ||||
C、2-
| ||||
D、
|
 4、如图所示,正方形ABCD中,E,F是对角线AC上两点,连接BE,BF,DE,DF,则添加下列哪一个条件可以判定四边形BEDF是菱形( )
4、如图所示,正方形ABCD中,E,F是对角线AC上两点,连接BE,BF,DE,DF,则添加下列哪一个条件可以判定四边形BEDF是菱形( )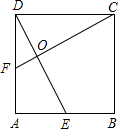 如图所示,正方形ABCD中,E为AB中点,F为AD中点,DE、CF交于O点,求证:DE⊥CF.
如图所示,正方形ABCD中,E为AB中点,F为AD中点,DE、CF交于O点,求证:DE⊥CF. 如图所示,正方形ABCD的边长为1,点E为AB的中点,以E为圆心,1为半径作圆,分别交AD,BC于M,N两点,与DC切于点P,则图中阴影部分面积是
如图所示,正方形ABCD的边长为1,点E为AB的中点,以E为圆心,1为半径作圆,分别交AD,BC于M,N两点,与DC切于点P,则图中阴影部分面积是 如图所示的正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
如图所示的正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题: