题目内容
如图直角坐标系中,△ABC的三个顶点都在小正方形的顶点上,则△ABC的面积为( )

| A、5 | ||
B、3
| ||
C、
| ||
D、3
|
分析:注意象限内点的特点,第二象限内的点横坐标为负,纵坐标为正,第四象限内的点横坐标为正,纵坐标为负,仔细观察图设直线AB与y=-1的交点为D,则△ABC的面积=△ADC的面积+△BCD的面积.
解答: 解:由图可知A(-1,2),B(1,-2),C(3,-1),
解:由图可知A(-1,2),B(1,-2),C(3,-1),
所以直线AB的解析式为:y=-2x
设直线AB与直线y=-1的交点为D,如右图示
则D(
,-1),
则CD的长为3-
=
,
A到CD的距离为3,B到CD的距离为1,
∴△ACD的面积为
CD×A到CD距离=
×
×3=
,
△BCD的面积为
×CD×B到CD的距离=
×
×1=
,
∴△ABC的面积=△ACD的面积+△BCD的面积=
+
=5;
故选A.
 解:由图可知A(-1,2),B(1,-2),C(3,-1),
解:由图可知A(-1,2),B(1,-2),C(3,-1),所以直线AB的解析式为:y=-2x
设直线AB与直线y=-1的交点为D,如右图示
则D(
| 1 |
| 2 |
则CD的长为3-
| 1 |
| 2 |
| 5 |
| 2 |
A到CD的距离为3,B到CD的距离为1,
∴△ACD的面积为
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 15 |
| 4 |
△BCD的面积为
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 4 |
∴△ABC的面积=△ACD的面积+△BCD的面积=
| 15 |
| 4 |
| 5 |
| 4 |
故选A.
点评:本题考查的是象限内点的性质以及函数图形的特征,需注意图形结合并能很好的运用图形将问题简便化.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 能请求出点E的坐标,如果不能请说明理由.
能请求出点E的坐标,如果不能请说明理由.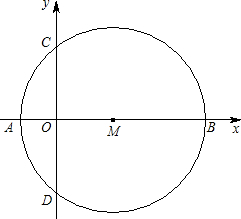 如图直角坐标系中,以M(3,0)为圆心的⊙M交x轴负半轴于A,交x轴正半轴于B,交y轴于C、D.
如图直角坐标系中,以M(3,0)为圆心的⊙M交x轴负半轴于A,交x轴正半轴于B,交y轴于C、D. (1)在如图直角坐标系中,描出点(9,1)(11,6)(16,8)(11,10)(9,15)(7,10)(2,8)(7,6)(9,1),并将各点用线段顺次连接起来.
(1)在如图直角坐标系中,描出点(9,1)(11,6)(16,8)(11,10)(9,15)(7,10)(2,8)(7,6)(9,1),并将各点用线段顺次连接起来. 有一个Rt△ABC,∠A=90°,∠B=60°,AB=1,将它放在如图直角坐标系中,使斜边BC在x轴上,直角顶点A在反比例函数y=-
有一个Rt△ABC,∠A=90°,∠B=60°,AB=1,将它放在如图直角坐标系中,使斜边BC在x轴上,直角顶点A在反比例函数y=-