题目内容
已知a=| 1 | ||
|
| 1 | ||
|
| b |
| a |
| a |
| b |
分析：先把a、b分母有理化，然后得到a+b=2
，ab=1；再把所求的分式通分变形得到原式=
，然后把a+b=2
，ab=1整体代入进行计算即可．
| 5 |
| (a+b)2 |
| ab |
| 5 |
解答：解：∵a=
，b=
，
∴a=
+2，b=
-2，
∴a+b=2
，ab=1，
原式=
+2
=
+2
=
，
∴当a+b=2
，ab=1，
原式=（2
）2=20．
故答案为20．
| 1 | ||
|
| 1 | ||
|
∴a=
| 5 |
| 5 |
∴a+b=2
| 5 |
原式=
| a 2+b2 |
| ab |
=
| (a+b) 2-2ab |
| ab |
=
| (a+b)2 |
| ab |
∴当a+b=2
| 5 |
原式=（2
| 5 |
故答案为20．
点评：本题考查了分式的化简求值：先把已知条件变形（分母有理化）得到两字母和与积的值，然后把所求的分式变形成这两字母和与积来表示的形式，再利用整体代入的方法代值进行计算．也考查了二次根式的化简求值．
练习册系列答案
相关题目
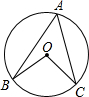如图，OB、OC是⊙O的半径，A是⊙O上一点，若已知∠B=15°，∠C=25°，则∠BOC=
前进中学校园内有一块如图所示的三角形空地，学校准备在它上面铺上草皮，已知∠A=