题目内容
 24、如图,△PQR和△P′Q′R′,是两个全等的等边三角形,它们的重叠部分是一个六边形ABCDEF,设这个六边形的边长为AB=a1,BC=b1,CD=a2,DE=b2,EF=a3,FA=b3.求证:a12+a22+a32=b12+b22+b32.
24、如图,△PQR和△P′Q′R′,是两个全等的等边三角形,它们的重叠部分是一个六边形ABCDEF,设这个六边形的边长为AB=a1,BC=b1,CD=a2,DE=b2,EF=a3,FA=b3.求证:a12+a22+a32=b12+b22+b32.分析:根据△PQR和△P′Q′R′是等边三角形,求证△AP′B∽△GQB∽△GQ′D∽△ERD∽△ER′F∽△APF,利用它们的面积比是相似比的平方,设比例系数为k,由于两正三角形重叠部分应有相等面积,故(a12+a22+a32)k=(b12+b22+b32)k,即可证明.
解答:解: 如右图所示,
如右图所示,
∵△PQR和△P′Q′R′是等边三角形,
∴∠P=∠Q=∠R=∠P′=∠Q′=∠R′=60°,
又∵∠ABP′=∠CBQ,∠BCQ=∠DCQ′,∠Q′DC=∠EDR,
∠DER=∠FER′,∠EFR′=∠AFP,∠FAP=∠BAP′,
∴△AP′B∽△GQB∽△GQ′D∽△ERD∽△ER′F∽△APF,
∴△AP′B∽△CQB∽△CQ′D∽△ERD∽ER′F∽APF,
它们的面积比是相似比的平方,设比例系数为k,
则S△AP′B=AB2k=a12•k,S△CQB=CB2•k=b12•k,
S△CQ′D=CD2•k=a22•k,S△ERD=ED2•k=b22•k,
S△ER′F=EF2•k=a32•k,S△APF=FA2•k=b32•k,
由于两正三角形重叠部分应有相等面积,
故(a12+a22+a32)k=(b12+b22+b32)k,
即a12+a22+a32=b12+b22+b32.
 如右图所示,
如右图所示,∵△PQR和△P′Q′R′是等边三角形,
∴∠P=∠Q=∠R=∠P′=∠Q′=∠R′=60°,
又∵∠ABP′=∠CBQ,∠BCQ=∠DCQ′,∠Q′DC=∠EDR,
∠DER=∠FER′,∠EFR′=∠AFP,∠FAP=∠BAP′,
∴△AP′B∽△GQB∽△GQ′D∽△ERD∽△ER′F∽△APF,
∴△AP′B∽△CQB∽△CQ′D∽△ERD∽ER′F∽APF,
它们的面积比是相似比的平方,设比例系数为k,
则S△AP′B=AB2k=a12•k,S△CQB=CB2•k=b12•k,
S△CQ′D=CD2•k=a22•k,S△ERD=ED2•k=b22•k,
S△ER′F=EF2•k=a32•k,S△APF=FA2•k=b32•k,
由于两正三角形重叠部分应有相等面积,
故(a12+a22+a32)k=(b12+b22+b32)k,
即a12+a22+a32=b12+b22+b32.
点评:此题考查学生对相似三角形的判定与性质和等边三角形的性质的理解和掌握,但是此题步骤繁琐,特别是多个三角形相似,而且用到相似比是面积比的平方,更给此题增加了难度,因此属于难题,

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 A、B两地相距50km,甲、乙两人在某日同时接到通知,都要从A到B地且行驶路线相同,甲骑自行车从A地出发驶往B地,乙也于同日骑摩托车从A地出发驶往B地,如图折线PQR和线段MN分别表示甲、乙两人所行驶的里程数s(km)与接到通知后的时间t(时)之间的函数关系的图象.
A、B两地相距50km,甲、乙两人在某日同时接到通知,都要从A到B地且行驶路线相同,甲骑自行车从A地出发驶往B地,乙也于同日骑摩托车从A地出发驶往B地,如图折线PQR和线段MN分别表示甲、乙两人所行驶的里程数s(km)与接到通知后的时间t(时)之间的函数关系的图象.
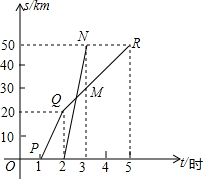 A、B两地相距50km,甲、乙两人在某日同时接到通知,都要从A到B地且行驶路线相同,甲骑自行车从A地出发驶往B地,乙也于同日骑摩托车从A地出发驶往B地,如图折线PQR和线段MN分别表示甲、乙两人所行驶的里程数s(km)与接到通知后的时间t(时)之间的函数关系的图象.
A、B两地相距50km,甲、乙两人在某日同时接到通知,都要从A到B地且行驶路线相同,甲骑自行车从A地出发驶往B地,乙也于同日骑摩托车从A地出发驶往B地,如图折线PQR和线段MN分别表示甲、乙两人所行驶的里程数s(km)与接到通知后的时间t(时)之间的函数关系的图象. 如图,△PQR和△P′Q′R′,是两个全等的等边三角形,它们的重叠部分是一个六边形ABCDEF,设这个六边形的边长为AB=a1,BC=b1,CD=a2,DE=b2,EF=a3,FA=b3.求证:a12+a22+a32=b12+b22+b32.
如图,△PQR和△P′Q′R′,是两个全等的等边三角形,它们的重叠部分是一个六边形ABCDEF,设这个六边形的边长为AB=a1,BC=b1,CD=a2,DE=b2,EF=a3,FA=b3.求证:a12+a22+a32=b12+b22+b32.