题目内容
16. 如图,已知:在⊙O中,弦AB为8,圆心O到AB的距离为3.
如图,已知:在⊙O中,弦AB为8,圆心O到AB的距离为3.(1)求圆的半径;
(2)若点P是AB上的一动点,试求OP最大值和最小值.
分析 (1)连接AO,过O作OD⊥AB,根据垂径定理可得AD=4,然后利用勾股定理计算出AO长即可;
(2)根据垂线段最短结合图形可得答案.
解答  解:(1)连接AO,过O作OD⊥AB,
解:(1)连接AO,过O作OD⊥AB,
∵弦AB为8,
∴AD=4,
∵圆心O到AB的距离为3,
∴DO=3,
∴AO=$\sqrt{D{O}^{2}+A{D}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5,
∴圆的半径是5;
(2)∵点P是AB上的一动点,
∴OP最大值是5,OP最小值是3.
点评 此题主要考查了垂径定理,关键是掌握垂直弦的直径平分这条弦,并且平分弦所对的两条弧.

练习册系列答案
相关题目
11.下列说法正确的是( )
| A. | 三个有理数相乘积为负数,则这三个数一定都是负数 | |
| B. | 两个有理数的和为零,则这两个数一定互为相反数 | |
| C. | 零是最小的有理数 | |
| D. | 两个有理数的和不可能比任何一个加数都小 |
1.水库管理人员为掌握水库蓄水情况,需要观测水库水位变化,如表是一周内水位高低的变化情况,用正数表示水位比前一天上升数,用负数表示水位比前一天下降数.
(1)问水库的水位在本周内是上升还是下降,幅度是多少?
(2)这一周内,哪一天水库的水位最高?哪一天的水位最低?最高水位比最低水位高多少?
| 星期 | 日 | 一 | 二 | 三 | 四 | 五 | 六 |
| 水位变化(cm) | 10 | -1 | -12 | 6 | -20 | -5 | 30 |
(2)这一周内,哪一天水库的水位最高?哪一天的水位最低?最高水位比最低水位高多少?
6.下列各式中,正确的是( )
| A. | -$\frac{1}{100}$>0 | B. | -$\frac{1}{5}$<-$\frac{1}{7}$ | C. | -6<-8 | D. | $\frac{1}{3}$<0.3 |
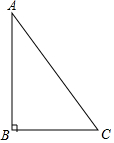 已知Rt△ABC中,∠B=90°
已知Rt△ABC中,∠B=90°