题目内容
13.小华和小敏站在高为4m的路灯左右两侧,已知小华的身高为1.6m,小敏的身高为1.5m,他们的影长都是2m.求他们相距多远.分析 先根据中心投影的定义画出几何图形,如图,AB=4m,DG=FH=2m,CD=1.5m,EF=1.6m,再证明△GCD∽△GAB,利用相似比可计算出DB=$\frac{10}{3}$m,接着证明△HEF∽△HAB,利用相似比计算出FB=3m,然后计算DB+BF即可.
解答  解:如图,AB=4m,DG=FH=2m,CD=1.5m,EF=1.6m,
解:如图,AB=4m,DG=FH=2m,CD=1.5m,EF=1.6m,
∵CD∥AB,
∴△GCD∽△GAB,
∴$\frac{GD}{GB}$=$\frac{CD}{AB}$,即$\frac{2}{2+DB}$=$\frac{1.5}{4}$,解得DB=$\frac{10}{3}$(m),
∵EF∥AB,
∴△HEF∽△HAB,
∴$\frac{HF}{HB}$=$\frac{EF}{AB}$,即$\frac{2}{2+FB}$=$\frac{1.6}{4}$,解得FB=3(m),
∴DF=DB+BF=$\frac{10}{3}$+3=$\frac{19}{3}$(m).
答:他们相距$\frac{19}{3}$m.
点评 本题考查了相似三角形的应用:常常构造“A”型或“X”型相似图,然后利用三角形的对应边成比例求相应线段的长.

练习册系列答案
相关题目
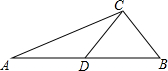 如图,在△ABC中,AB边上的中线CD=3,AB=6,BC+AC=8,
如图,在△ABC中,AB边上的中线CD=3,AB=6,BC+AC=8, 如图,在直角坐标系中,△ABC的各顶点坐标为A(-1,1),B(2,3),C(0,3).现以坐标原点为位似中心,位似比为$\frac{2}{3}$,作△ABC的位似图形△A′B′C′,则△A′B′C′的顶点坐标A′、B′、C′的坐标各是多少?
如图,在直角坐标系中,△ABC的各顶点坐标为A(-1,1),B(2,3),C(0,3).现以坐标原点为位似中心,位似比为$\frac{2}{3}$,作△ABC的位似图形△A′B′C′,则△A′B′C′的顶点坐标A′、B′、C′的坐标各是多少?