题目内容
13.已知三角形三边长分别为15、17、8,则此三角形的最长边上的高为( )| A. | 17 | B. | $\frac{120}{17}$ | C. | $\frac{136}{15}$ | D. | 15 |
分析 首先根据勾股定理的逆定理判定此三角形是直角三角形,然后根据直角三角形的面积计算方法即可得出结论.
解答 解:∵82+152=172,
∴此三角形是直角三角形,且直角边为15,8,
∴此三角形的最长边上的高=$\frac{15×8}{17}$=$\frac{120}{17}$.
故选B.
点评 本题考查的是勾股定理的逆定理,先根据题意判断出三角形的形状是解答此题的关键.

练习册系列答案
相关题目
8. 如图,将正方体的平面展开图重新折成正方体后,“快”字对面的字是( )
如图,将正方体的平面展开图重新折成正方体后,“快”字对面的字是( )
 如图,将正方体的平面展开图重新折成正方体后,“快”字对面的字是( )
如图,将正方体的平面展开图重新折成正方体后,“快”字对面的字是( )| A. | 新 | B. | 年 | C. | 祝 | D. | 乐 |
18.如图1,A,B,C是郑州市二七区三个垃圾存放点,点B,C分别位于点A的正北和正东方向,AC=40米.八位环卫工人分别测得的BC长度如下表:
他们又调查了各点的垃圾量,并绘制了下列尚不完整的统计图2,图3:
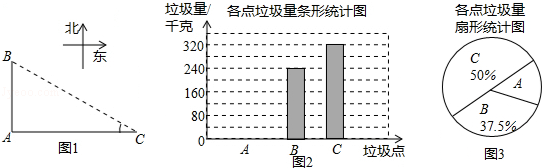
(1)求表中BC长度的平均数$\overline{x}$、中位数、众数;
(2)求A处的垃圾量,并将图2补充完整;
(3)用(1)中的$\overline{x}$作为BC的长度,要将A处的垃圾沿道路AB都运到B处,已知运送1千克垃圾每米的费用为0.005元,求运垃圾所需的费用.(注:$\sqrt{3}$=1.732)
| 甲 | 乙 | 丙 | 丁 | 戊 | 戌 | 申 | 辰 | |
| BC(单位:米) | 84 | 76 | 78 | 82 | 70 | 84 | 86 | 80 |

(1)求表中BC长度的平均数$\overline{x}$、中位数、众数;
(2)求A处的垃圾量,并将图2补充完整;
(3)用(1)中的$\overline{x}$作为BC的长度,要将A处的垃圾沿道路AB都运到B处,已知运送1千克垃圾每米的费用为0.005元,求运垃圾所需的费用.(注:$\sqrt{3}$=1.732)
5.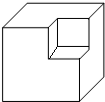 从棱长为4a的正方体中,挖去一个棱长为2a的小正方体,得到一个如图所示的几何体,则该几何体的体积是( )
从棱长为4a的正方体中,挖去一个棱长为2a的小正方体,得到一个如图所示的几何体,则该几何体的体积是( )
 从棱长为4a的正方体中,挖去一个棱长为2a的小正方体,得到一个如图所示的几何体,则该几何体的体积是( )
从棱长为4a的正方体中,挖去一个棱长为2a的小正方体,得到一个如图所示的几何体,则该几何体的体积是( )| A. | 4a3 | B. | 8a3 | C. | 56a3 | D. | 58a3 |
3.若|a-3|-3+a=0,则a的取值范围是( )
| A. | a≤3 | B. | a<3 | C. | a=3 | D. | a≥3 |
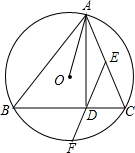 如图,已知△ABC内接于⊙O,AD⊥BC于D,E为AC的中点,延长ED交⊙O于F.
如图,已知△ABC内接于⊙O,AD⊥BC于D,E为AC的中点,延长ED交⊙O于F.