Question

16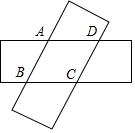．如图，由两个长为9，宽为3的全等矩形叠合而得到四边形ABCD，则四边形ABCD面积的最大值是（　　）

• A． 15
• B． 16
• C． 19
• D． 20

Answer 1

分析 首先根据图1，证明四边形ABCD是菱形；然后判断出菱形的一条对角线为矩形的对角线时，四边形ABCD的面积最大，设AB=BC=x，则BE=9-x，利用勾股定理求出x的值，即可求出四边形ABCD面积的最大值是多少．

解答 解：如图1，作AE⊥BC于E，AF⊥CD于F，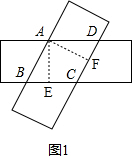
，
∵AD∥BC，AB∥CD，
∴四边形ABCD是平行四边形，
∵两个矩形的宽都是3，
∴AE=AF=3，
∵S_{四边形ABCD}=AE•BC=AF•CD，
∴BC=CD，
∴平行四边形ABCD是菱形．

如图2，
，
设AB=BC=x，则BE=9-x，
∵BC²=BE²+CE²，
∴x²=（9-x）²+3²，
解得x=5，
∴四边形ABCD面积的最大值是：
5×3=15．
故选：A．

点评 此题主要考查了菱形的判定和性质，矩形的性质和应用，以及勾股定理的应用，要熟练掌握．