题目内容
【题目】如图,反比例函数![]() 的图像经过第二象限内的点
的图像经过第二象限内的点![]() ,
,![]() 轴于点
轴于点![]() ,
,![]() 的面积为2.若直线
的面积为2.若直线![]() 经过点
经过点![]() ,并且经过反比例函数
,并且经过反比例函数![]() 的图像上另一点
的图像上另一点![]() .
.
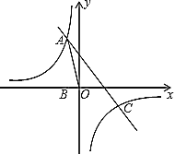
(1)求反比例函数![]() 与直线
与直线![]() 的解析式;
的解析式;
(2)连接![]() ,求
,求![]() 的面积;
的面积;
(3)不等式![]() 的解集为_________
的解集为_________
(4)若![]() 在
在![]()
![]() 图像上,且满足
图像上,且满足![]() ,则
,则![]() 的取值范围是_________.
的取值范围是_________.
【答案】(1)![]() ;
;![]() (2)3 (3)
(2)3 (3)![]() 或
或![]() (4)
(4)![]() 或x<0
或x<0
【解析】
(1)根据![]() 的几何意义即可求出
的几何意义即可求出![]() ;求出
;求出![]() 后利用交点
后利用交点![]() 即可求出一次函数
即可求出一次函数
(2)利用割补法即可求出面积
(3)根据A,C的坐标,结合图象即可求解;
(4)先求出![]() 时,
时,![]() ,再观察图像即可求解.
,再观察图像即可求解.
(1)∵点![]() 在第二象限内,
在第二象限内,
∴![]() ,
,![]() ,
,
∴![]() 即:
即:![]() ,解得
,解得![]() ,
,
∴![]() ,
,
∵点![]() ,在反比例函数
,在反比例函数![]() 的图像上,
的图像上,
∴![]() ,解得
,解得![]() ,
,
∵反比例函数为![]() ,
,
又∵反比例函数![]() 的图像经过
的图像经过![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴![]() ,
,
∵直线![]() 过点
过点![]() ,
,![]() ,
,
∴![]() 解方程组得
解方程组得![]() ,
,
∴直线![]() 的解析式为;
的解析式为;![]() ;
;
(2)![]()
当![]() 时,
时,![]() ,
,![]() ,
,
∴![]() 与
与![]() 轴的交点坐标为
轴的交点坐标为![]()
设直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,
,
则![]()
∴![]()
![]()
![]()
(3)由题:![]()
由图像可知:当![]() 或
或![]() 时,符合条件;
时,符合条件;
故答案为:![]() 或
或![]() ;
;
(4)![]() 时,
时,![]() ,结合图像可知:当
,结合图像可知:当![]() ,则
,则![]() 的取值范围是
的取值范围是![]() 或x<0.
或x<0.
故答案为:![]() 或x<0.
或x<0.

练习册系列答案
相关题目