题目内容
 如图,两座建筑物AB及CD,其中A,C距离为50米,在AB的顶点B处测得CD的顶部D的仰角β=30°,测得其底部C的俯角α=60°,求两座建筑物AB及CD的高度(精确到0.1米).
如图,两座建筑物AB及CD,其中A,C距离为50米,在AB的顶点B处测得CD的顶部D的仰角β=30°,测得其底部C的俯角α=60°,求两座建筑物AB及CD的高度(精确到0.1米).
解:由图可知:∠α=60°,∠β=30°,
∵四边形ABEC是平行四边形
∴BE=AC=50,AB=CE,
在Rt△BCE中,
∵tanα= ,
,
∴CE=BE•tanα=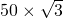 =
= ,
,
∴AB= ≈86.6(米)
≈86.6(米)
在Rt△BDE中,
∵tanβ= ,
,
∴DE=BE•tanβ=50× =
= ,
,
∴CD=CE+DE= +
+ ≈115.5(米)
≈115.5(米)
答:建筑物AB的高度约为86.6米,建筑物CD的高度约为115.5米.
分析:在直角三角形BDE和直角三角形BEC中,分别用BE表示DE,EC的长,代入BE的值和已知角的三角函数值即可求出AB和CD的高度.
点评:本题考查俯角、仰角的知识,难度适中,要求学生能借助其关系构造直角三角形并解直角三角形.
∵四边形ABEC是平行四边形
∴BE=AC=50,AB=CE,
在Rt△BCE中,
∵tanα=
 ,
,∴CE=BE•tanα=
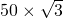 =
= ,
,∴AB=
 ≈86.6(米)
≈86.6(米)在Rt△BDE中,
∵tanβ=
 ,
,∴DE=BE•tanβ=50×
 =
= ,
,∴CD=CE+DE=
 +
+ ≈115.5(米)
≈115.5(米)答:建筑物AB的高度约为86.6米,建筑物CD的高度约为115.5米.
分析:在直角三角形BDE和直角三角形BEC中,分别用BE表示DE,EC的长,代入BE的值和已知角的三角函数值即可求出AB和CD的高度.
点评:本题考查俯角、仰角的知识,难度适中,要求学生能借助其关系构造直角三角形并解直角三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,两座建筑物AB与CD,其水平距离BD为30米,在从AB的顶点A处用高1米的测角仪AE测得CD的顶部C的仰角α=30°,测得其底部D的俯角β=45°,求两座建筑物AB与CD的高.
如图,两座建筑物AB与CD,其水平距离BD为30米,在从AB的顶点A处用高1米的测角仪AE测得CD的顶部C的仰角α=30°,测得其底部D的俯角β=45°,求两座建筑物AB与CD的高. (2013•从化市一模)如图,两座建筑物AB及CD,其中A,C距离为50米,在AB的顶点B处测得CD的顶部D的仰角β=30°,测得其底部C的俯角α=60°,求两座建筑物AB及CD的高度(精确到0.1米).
(2013•从化市一模)如图,两座建筑物AB及CD,其中A,C距离为50米,在AB的顶点B处测得CD的顶部D的仰角β=30°,测得其底部C的俯角α=60°,求两座建筑物AB及CD的高度(精确到0.1米).

