题目内容
| |||||||||||||||
答案:
解析:
解析:
(1) |
等腰梯形ABCD,得AB=DC,∠A=∠D.由M分别是AD的中点,得AM=MD.从而得△ABM≌△DCM. |
(2) |
由△ABM≌△DCM,得MB=MC. 又E、F分别是BM、CM的中点, 所以ME=MF,由MB-MC,得△MBC为等腰三角形. N是BC的中点,所以MN⊥BC. 由ME=BE,得NE=ME. 同理得NF=MF. 故四边形MENF是菱形. |
(3) |
MN= |

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目


 16、如图,已知等腰梯形ABCD的中位线EF的长为5,腰AD的长为4,则这个等腰梯形的周长为
16、如图,已知等腰梯形ABCD的中位线EF的长为5,腰AD的长为4,则这个等腰梯形的周长为 30、如图所示,等腰梯形ABCD中,AD∥BC,BD⊥DC,点E是BC边的中点,ED∥AB,则∠BCD等于( )
30、如图所示,等腰梯形ABCD中,AD∥BC,BD⊥DC,点E是BC边的中点,ED∥AB,则∠BCD等于( ) 如图,已知等腰梯形ABCD中,AD∥BC,AD=2,BC=5,∠B=60°,求梯形ABCD的周长.
如图,已知等腰梯形ABCD中,AD∥BC,AD=2,BC=5,∠B=60°,求梯形ABCD的周长.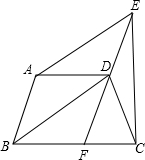 如图所示,等腰梯形ABCD中,AD∥BC,DF∥AB交BC于F点,AE∥BD交FD的延长线于E点.
如图所示,等腰梯形ABCD中,AD∥BC,DF∥AB交BC于F点,AE∥BD交FD的延长线于E点.