题目内容
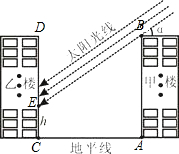
 如图为某小区的两幢10层住宅楼,由地面向上依次为第1层、第2层、…、第10层,每层的高度为3m,两楼间的距离AC=30m.假设某一时刻甲楼AB落在乙楼的影子长为EC,太阳光线与水平线的夹角为α,且在这一时段内α每小时增加10°.
如图为某小区的两幢10层住宅楼,由地面向上依次为第1层、第2层、…、第10层,每层的高度为3m,两楼间的距离AC=30m.假设某一时刻甲楼AB落在乙楼的影子长为EC,太阳光线与水平线的夹角为α,且在这一时段内α每小时增加10°.(1)当α=30°时,甲楼楼顶B的影子落在乙楼的第几层?
(2)在(1)的基础上,问:几小时后,甲楼的影子刚好不影响乙楼采光?
分析:(1)过点E作EF⊥AB于点F,根据锐角三角函数的定义可得出BF的长,由AF=AB-BF即可得出结论;
(2)先求出∠BCA的度数,再根据α每小时增加10°即可得出结论.
(2)先求出∠BCA的度数,再根据α每小时增加10°即可得出结论.
解答: 解:(1)过点E作EF⊥AB于点F,
解:(1)过点E作EF⊥AB于点F,
∵∠BEF=∠α=30°,
∴EF=
BF,
∵AC=EF=30m,
∴BF=
=10
m,
AF=AB-BF=30-10
≈12.64m,
∴甲楼楼顶B的影子落在乙楼的第五层;
(2)如图,AC=30m,BA=30m,
∴∠BCA=45°,
∴
=1.5(小时).
∴1.5小时后,甲楼的影子刚好不影响乙楼采光.
 解:(1)过点E作EF⊥AB于点F,
解:(1)过点E作EF⊥AB于点F,∵∠BEF=∠α=30°,
∴EF=
| 3 |
∵AC=EF=30m,
∴BF=
| 30 | ||
|
| 3 |
AF=AB-BF=30-10
| 3 |
∴甲楼楼顶B的影子落在乙楼的第五层;
(2)如图,AC=30m,BA=30m,

∴∠BCA=45°,
∴
| 45°-30° |
| 10° |
∴1.5小时后,甲楼的影子刚好不影响乙楼采光.
点评:本题考查的是解直角三角形的应用,熟知锐角三角函数的定义是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 时起几小时后甲楼的影子刚好不影响乙楼采光?
时起几小时后甲楼的影子刚好不影响乙楼采光?

 取1.73)
取1.73)
 取1.73)
取1.73)