题目内容
【题目】对于平面直角坐标系![]() 中的点
中的点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() (其中
(其中![]() 为常数,且
为常数,且![]() ),则称点
),则称点![]() 为点
为点![]() 的“
的“![]() 属派生点”.例如:
属派生点”.例如:![]() 的“2属派生点”为
的“2属派生点”为![]() ,即
,即![]() .
.
(l)求点![]() 的“3属派生点”
的“3属派生点”![]() 的坐标:
的坐标:
(2)若点![]() 的“5属派生点”
的“5属派生点”![]() 的坐标为
的坐标为![]() ,求点
,求点![]() 的坐标:
的坐标:
(3)若点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 的“收属派生点”为
的“收属派生点”为![]() 点,且线段
点,且线段![]()
![]() 的长度为线段
的长度为线段![]() 长度的2倍,求k的值.
长度的2倍,求k的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据“k属派生点”计算可得;
(2)设点P的坐标为(x、y),根据“k属派生点”定义及P′的坐标列出关于x、y的方程组,解之可得;
(3)先得出点P′的坐标为(a,ka),由线段PP′的长度为线段OP长度的2倍列出方程,解之可得.
解:(1)点![]() 的“3属派生点”
的“3属派生点”![]() 的坐标为
的坐标为![]() ,即
,即![]()
(2)设![]() ,
,
依题意,得方程组:![]() ,
,
解得![]() ,.
,.
∴点![]()
(3)∵点P在x轴的正半轴上,
∴b=0,a>0.
∴点P的坐标为(a,0),点P′的坐标为(a,ka)
∴线段PP′的长为P′到x轴距离为|ka|.
∵P在x轴正半轴,线段OP的长为a,
∴|ka|=2a,即|k|=2,
∴k=±2.

练习册系列答案
相关题目
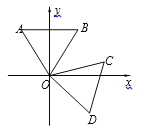
【题目】下列各图中,直线都交于一点,请探究交于-一点的直线的条数与所形成的对顶角的对数之间的规律。
(1)请观察上图并填写下表
交于一点的直线的条数 | 2 | 3 | 4 |
对顶角的对数 |
(2)若n条直线交于一点,则共有_____________对对顶角(用含n的代数式表示).
(3)当100条直线交于一点时,则共有_____________对对顶角