题目内容
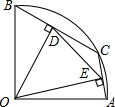 如图,在半径为R(R为常数)的扇形AOB中,∠AOB=90°,点C在
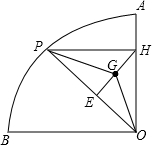
如图,在半径为R(R为常数)的扇形AOB中,∠AOB=90°,点C在 上从点A向点B运动(不与点A、B重合),连结AC,BC,OD⊥BC,OE⊥AC,垂足分别为D、E,则线段DE的长度
上从点A向点B运动(不与点A、B重合),连结AC,BC,OD⊥BC,OE⊥AC,垂足分别为D、E,则线段DE的长度
- A.先变大后变小
- B.不变
- C.先变小后变大
- D.不能确定
B
分析:连接AB,求出AB长,根据垂径定理求出BD=DC,AE=EC,得出DE是△CBA的中位线,求出DE= AB即可.
AB即可.
解答: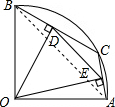
连接AB,根据勾股定理得:AB= =
= R,
R,
∵OD⊥BC,OE⊥AC,OD、OE过O,
∴BD=DC,AE=EC,
∴DE= AB=
AB= ×
× R=
R= R,
R,
即不管C点怎样运动,线段DE的长度不变,都等于 R,
R,
故选B.
点评:本题考查了勾股定理,垂径定理,三角形的中位线的应用,关键是得出DE是三角形CAB的中位线.
分析:连接AB,求出AB长,根据垂径定理求出BD=DC,AE=EC,得出DE是△CBA的中位线,求出DE=
 AB即可.
AB即可.解答:

连接AB,根据勾股定理得:AB=
 =
= R,
R,∵OD⊥BC,OE⊥AC,OD、OE过O,
∴BD=DC,AE=EC,
∴DE=
 AB=
AB= ×
× R=
R= R,
R,即不管C点怎样运动,线段DE的长度不变,都等于
 R,
R,故选B.
点评:本题考查了勾股定理,垂径定理,三角形的中位线的应用,关键是得出DE是三角形CAB的中位线.

练习册系列答案
相关题目
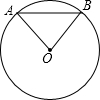 如图,在半径为5的⊙O中,若弦AB=8,则△AOB的面积为( )
如图,在半径为5的⊙O中,若弦AB=8,则△AOB的面积为( )| A、24 | B、16 | C、12 | D、8 |
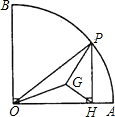 心为G.
心为G. 如图,在半径为1的⊙O中,AB为直径,C为弧AB的中点,D为弧CB的三等分点,且弧DB的长等于弧CD长的两倍,连接AD并延长交⊙O的切线CE于点E(C为切点),则AE的长为
如图,在半径为1的⊙O中,AB为直径,C为弧AB的中点,D为弧CB的三等分点,且弧DB的长等于弧CD长的两倍,连接AD并延长交⊙O的切线CE于点E(C为切点),则AE的长为
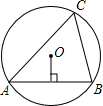 如图,在半径为2的⊙O中,圆心0到弦AB的距离为1,C为AB上方圆弧上任意一点,则∠ACB=
如图,在半径为2的⊙O中,圆心0到弦AB的距离为1,C为AB上方圆弧上任意一点,则∠ACB=