题目内容
a、b、c三个有理数满足a<0<b<c,且a+b+c=1, ,
, ,
, ,则M、N、P之间的大小关系是________.
,则M、N、P之间的大小关系是________.
M<P<N
分析:分别得到b+c,a+c,a+b的值,代入所给代数式,进而比较即可.
解答:由题意得:b+c=1-a,
a+c=1-b,
a+b=1-c,
∴M=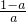 =
= -1,
-1,
N= -1,
-1,
P= -1,
-1,
∵a<0<b<c,
∴ 最小,
最小,
∴M最小,
∵0<b<c,
∴ >
> ,
,
∴N<P,
∴M<P<N,
故答案为:M<P<N.
点评:考查有理数的大小比较;根据所给等式把所给代数式进行化简是解决本题的突破点.
分析:分别得到b+c,a+c,a+b的值,代入所给代数式,进而比较即可.
解答:由题意得:b+c=1-a,
a+c=1-b,
a+b=1-c,
∴M=
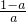 =
= -1,
-1,N=
 -1,
-1,P=
 -1,
-1,∵a<0<b<c,
∴
 最小,
最小,∴M最小,
∵0<b<c,
∴
 >
> ,
,∴N<P,
∴M<P<N,
故答案为:M<P<N.
点评:考查有理数的大小比较;根据所给等式把所给代数式进行化简是解决本题的突破点.

练习册系列答案
相关题目
