题目内容
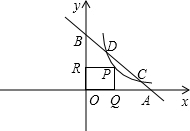
 直线l过点A(4,0)和B(0,4)两点,它与二次函数y=ax2的图象在第一象限内交于点P,若S△AOP=
直线l过点A(4,0)和B(0,4)两点,它与二次函数y=ax2的图象在第一象限内交于点P,若S△AOP= ,求二次函数关系式.
,求二次函数关系式.
解:设直线为:y=kx+b,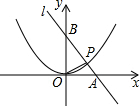
∵直线l过点A(4,0)和B(0,4)两点,
∴4k+b=0,b=4
∴y=-x+4,
∵S△AOP= ,
,
∴ ×4×yp=
×4×yp= ,
,
∴yp= ,
,
∴ =-x+4,
=-x+4,
解得x= ,
,
把点P的坐标( ,
, )代入y=ax2,
)代入y=ax2,
解得a= ,
,
∴y=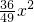 .
.
分析:由题意直线l过点A(4,0)和B(0,4)两点,根据待定系数法求出直线AB的解析式,再很据S△AOP= ,求出点P的纵坐标,然后将它代入直线AB的解析式,求出点P的横坐标,最后把点P的坐标代入y=ax2,运用待定系数法即可求出二次函数的解析式.
,求出点P的纵坐标,然后将它代入直线AB的解析式,求出点P的横坐标,最后把点P的坐标代入y=ax2,运用待定系数法即可求出二次函数的解析式.
点评:此题考查一次函数和二次函数的基本性质及其对称轴和顶点坐标,运用待定系数法求抛物线的解析式,同时也考查了学生的计算能力.

∵直线l过点A(4,0)和B(0,4)两点,
∴4k+b=0,b=4
∴y=-x+4,
∵S△AOP=
 ,
,∴
 ×4×yp=
×4×yp= ,
,∴yp=
 ,
,∴
 =-x+4,
=-x+4,解得x=
 ,
,把点P的坐标(
 ,
, )代入y=ax2,
)代入y=ax2,解得a=
 ,
,∴y=
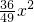 .
.分析:由题意直线l过点A(4,0)和B(0,4)两点,根据待定系数法求出直线AB的解析式,再很据S△AOP=
 ,求出点P的纵坐标,然后将它代入直线AB的解析式,求出点P的横坐标,最后把点P的坐标代入y=ax2,运用待定系数法即可求出二次函数的解析式.
,求出点P的纵坐标,然后将它代入直线AB的解析式,求出点P的横坐标,最后把点P的坐标代入y=ax2,运用待定系数法即可求出二次函数的解析式.点评:此题考查一次函数和二次函数的基本性质及其对称轴和顶点坐标,运用待定系数法求抛物线的解析式,同时也考查了学生的计算能力.

练习册系列答案
相关题目
 D两点,P为双曲线
D两点,P为双曲线 PQ⊥O1O2,交O1O2于点K,且
PQ⊥O1O2,交O1O2于点K,且