题目内容
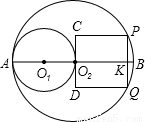
如图,以1为半径的⊙O1与以2为半径的⊙O2内切于点A,直线O1O2过点A,且交⊙O2于另一点B,⊙O2的弦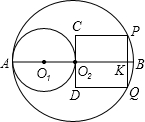 PQ⊥O1O2,交O1O2于点K,且PK=
PQ⊥O1O2,交O1O2于点K,且PK=| 1 | 2 |
(1)求圆心距O1O2;
(2)求四边形PCDQ的边长;
(3)若一动点H由点Q出发,沿四边形的边QP、PC、CD移动到点D,设动点H移动的路程为x,△DQH的面积为y,求y与x之间的函数解析式,并写出自变量x的取值范围.
分析:(1)根据题意,可知两圆内切,则圆心距等于两圆半径之差;
(2)首先可以证明该四边形是正方形,设正方形PCDQ的边长为x.连接O2P,根据勾股定理列方程求解;
(3)根据运动的路径,显然需要考虑三种情况:H点在QP边上移动时,即0≤x<
;H点在PC边上移动时,即
≤x<
;H点在CD边上移动时,即
≤x<
.
根据三角形的面积公式分别找到三角形的底边及其边上的高进行计算.
(2)首先可以证明该四边形是正方形,设正方形PCDQ的边长为x.连接O2P,根据勾股定理列方程求解;
(3)根据运动的路径,显然需要考虑三种情况:H点在QP边上移动时,即0≤x<
| 4 |
| 5 |
| 5 |
| 4 |
| 5 |
| 5 |
| 8 |
| 5 |
| 5 |
| 8 |
| 5 |
| 5 |
| 12 |
| 5 |
| 5 |
根据三角形的面积公式分别找到三角形的底边及其边上的高进行计算.
解答: 解:(1)O1O2=2-1=1.
解:(1)O1O2=2-1=1.
(2)∵CD切⊙O1于O2,
∴CD⊥O1O2,
又PQ⊥O1O2,
∴CD∥PQ.
∵PC∥O1O2,QD∥O1O2,
∴PC∥QD,PC⊥QP.
∵PK=
O2K=
PC=
PQ,
∴PC=PQ.
故四边形PCDQ是正方形.
设正方形PCDQ的边长为x,
则PK=
x,O2K=x,
由O2P2=O2K2+PK2,得
22=x2+(
)2,
解得,x=±
,舍去x=-
.
∴这个四边形四条边的长都是
.



(3)当H点在QP边上移动时,则QH=x;
∴y=
•(
)x=
x(0≤x<
);
当H点在PC边上移动时,
∴y=
•(
)2=
(
≤x<
);
当H点在CD边上移动时,DH=3×
-x
∴y=
×
×(
-x)=-
x+
(
≤x<
).
综上所述y=
.
 解:(1)O1O2=2-1=1.
解:(1)O1O2=2-1=1.(2)∵CD切⊙O1于O2,
∴CD⊥O1O2,
又PQ⊥O1O2,
∴CD∥PQ.
∵PC∥O1O2,QD∥O1O2,
∴PC∥QD,PC⊥QP.
∵PK=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴PC=PQ.
故四边形PCDQ是正方形.
设正方形PCDQ的边长为x,
则PK=
| 1 |
| 2 |
由O2P2=O2K2+PK2,得
22=x2+(
| x |
| 2 |
解得,x=±
| 4 |
| 5 |
| 5 |
| 4 |
| 5 |
| 5 |
∴这个四边形四条边的长都是
| 4 |
| 5 |
| 5 |



(3)当H点在QP边上移动时,则QH=x;
∴y=
| 1 |
| 2 |
| 4 |
| 5 |
| 5 |
| 2 |
| 5 |
| 5 |
| 4 |
| 5 |
| 5 |
当H点在PC边上移动时,
∴y=
| 1 |
| 2 |
| 4 |
| 5 |
| 5 |
| 8 |
| 5 |
| 4 |
| 5 |
| 5 |
| 8 |
| 5 |
| 5 |
当H点在CD边上移动时,DH=3×
| 4 |
| 5 |
| 5 |
∴y=
| 1 |
| 2 |
| 4 |
| 5 |
| 5 |
| 12 |
| 5 |
| 5 |
| 2 |
| 5 |
| 5 |
| 24 |
| 5 |
| 8 |
| 5 |
| 5 |
| 12 |
| 5 |
| 5 |
综上所述y=
|
点评:熟悉相切两圆的性质:两圆内切,则圆心距等于两圆半径之差;两圆外切,圆心距等于两圆半径之和.掌握正方形的判定方法,能够分别画出不同动态时一种静态时的位置,进行分析计算图形的面积.

练习册系列答案
相关题目
 PQ⊥O1O2,交O1O2于点K,且
PQ⊥O1O2,交O1O2于点K,且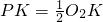 ,PC∥O1O2,QD∥O1O2,PC、QD分别交过点O2的⊙O1的切线于点C、D.
,PC∥O1O2,QD∥O1O2,PC、QD分别交过点O2的⊙O1的切线于点C、D. O2K,PC∥O1O2,QD∥O1O2,PC、QD分别交过点O2的⊙O1的切线于点C、D。
O2K,PC∥O1O2,QD∥O1O2,PC、QD分别交过点O2的⊙O1的切线于点C、D。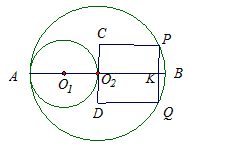
 ,PC∥O1O2,QD∥O1O2,PC、QD分别交过点O2的⊙O1的切线于点C、D.
,PC∥O1O2,QD∥O1O2,PC、QD分别交过点O2的⊙O1的切线于点C、D.
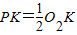 ,PC∥O1O2,QD∥O1O2,PC、QD分别交过点O2的⊙O1的切线于点C、D.
,PC∥O1O2,QD∥O1O2,PC、QD分别交过点O2的⊙O1的切线于点C、D.