题目内容
11．
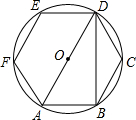如图所示，正六边形ABCDEF内接于圆O，则cos∠ADB的值为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{2}}}{2}$ | C． | $\frac{{\sqrt{3}}}{2}$ | D． | $\frac{{\sqrt{3}}}{3}$ |
分析 先根据正六边形的性质求出∠ADB的度数，再由特殊角的三角函数值即可得出结论．
解答 解：∵正六边形ABCDEF内接于圆O
∴$\widehat{AB}$的度数等于360°÷6=60°
∴∠ADB=30°，
∴cos∠ADB=cos30°=$\frac{\sqrt{3}}{2}$．
故选C．
点评 本题考查的是正多边形和圆，熟知正六边形的性质是解答此题的关键．
练习册系列答案
超能学典应用题题卡系列答案
相关题目
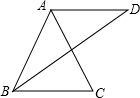如图，已知AB=AC=AD，且AD∥BC，试说明∠C与∠D之间的关系．
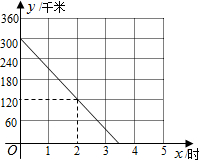A、B两座城市之间有一条高速公路，甲、乙两辆汽车同时分别从这条路两端的入口处驶入，并始终在高速公路上正常行驶．甲车驶往B城，乙车驶往A城，甲车在行驶过程中速度始终不变．甲车距B城高速公路入口处的距离y（千米）与行驶时间x（时）之间的关系如图．
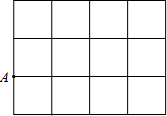在如图所示的4×3网格中，每个小正方形的边长为1，正方形顶点叫格点，连结两个网格格点的线段叫网格线段．点A固定在格点上．