题目内容
【题目】如图,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与CD的延长线交于点A, ![]() ,OE交BC于点F.
,OE交BC于点F.
(1)求证:OE∥BD;
(2)当⊙O的半径为5, ![]() 时,求EF的长.
时,求EF的长.
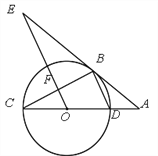
【答案】(1)证明见解析;(2)EF的长为![]()
【解析】试题分析:(1)连接OB,利用已知条件和切线的性质证明;
(2)根据锐角三角函数和相似三角形的性质,直接求解即可.
试题解析:(1)连接OB, ∵CD为⊙O的直径 , ![]()
![]() .
.
∵AE是⊙O的切线, ![]()
![]() .
. ![]()
![]() .
.
∵OB、OC是⊙O的半径, ![]() OB=OC. ∴
OB=OC. ∴![]() . ∴
. ∴![]() .
.
∵![]() ,∴
,∴![]() . ∴ OE∥BD.
. ∴ OE∥BD.
(2)由(1)可得sin∠C= ∠DBA= ![]() ,在Rt△
,在Rt△![]() 中, sin∠C =
中, sin∠C =![]() ,OC=5,
,OC=5,
![]() ∴
∴![]()
∵![]() ,
, ![]() △CBD∽△EBO.
△CBD∽△EBO.
∴![]()
∴![]() .
.
∵OE∥BD,CO=OD,
∴CF=FB.
∴![]() .
.
∴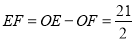

练习册系列答案
相关题目