Question

如图，ABCD是平行四边形，AB是⊙O的直径，点D在⊙O上AD=OA=1，则图中阴影部分的面积为

1. A.
   
2. B.
   
3. C.
   
4. D.
   

Answer 1

A
分析：根据平行四边形的性质以及等边三角形的判定得出3个等边三角形全等，进而得出阴影部分面积等于△BCE面积，求出即可．
解答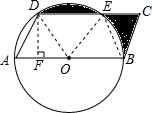：解：连接DO，EO，BE，过点D作DF⊥AB于点F，
∵AD=OA=1，
∴AD=AO=DO，
∴△AOD是等边三角形，
∵四边形ABCD是平行四边形，
∴DC∥AB，
∴∠CDO=∠DOA=60°，
∴△ODE是等边三角形，
同理可得出△OBE是等边三角形且3个等边三角形全等，
∴阴影部分面积等于△BCE面积，
∵DF=ADsin60°=，DE=EC=1，
∴图中阴影部分的面积为：××1=．
故选：A．
点评：此题考查了组合图形的面积，关键是得出阴影部分面积等于△BCE面积．