题目内容
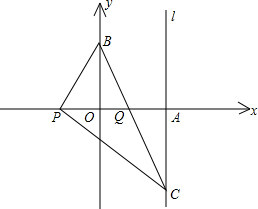
直角坐标系中,A(1,1),在坐标轴上找点B使△AOB为等腰三角形的点共有个.
- A.6
- B.7
- C.8
- D.9
C
分析:题中没有指明AO,BO,AB是底还是腰,故应该分情况进行分析,注意不但要考虑到AO,BO,AB是底还是腰,而且要考虑A,B是在正半轴还是在负半轴.
解答:(1)当AO,BO为腰时,
①当AO=BO(B在Y轴正半轴上),
∵点A坐标为(1,1),O为坐标原点,
∴OA=OB= ,
,
∴B1=(0, ),
),
②当AO=BO(B在Y轴负半轴上),
同理:B2=(0,- ).
).
③当AO=BO(B在X轴正半轴上),
同理:B3=( ,0).
,0).
④当AO=BO(B在X轴负半轴上),
同理:B4=(- ,0).
,0).
(2)当AO,AB为腰时,
⑤当AO=BO(B在Y轴正半轴上),
∵点A坐标为(1,1),O为坐标原点,
∴B5=(0,2).
⑥当AO=BO(B在X轴正半轴上),
同理:B6=(2,0).
(3)当AO为底时,
⑦AB=BO(B在Y轴正半轴上),
同理:B7=(0,1).
⑧当AB=BO(B在X轴正半轴上),
同理:B8=(1,0).
故选C.
点评:此题主要考查等腰三角形的性质及坐标与图形性质的综合运用,注意分类讨论思想的运用.
分析:题中没有指明AO,BO,AB是底还是腰,故应该分情况进行分析,注意不但要考虑到AO,BO,AB是底还是腰,而且要考虑A,B是在正半轴还是在负半轴.
解答:(1)当AO,BO为腰时,
①当AO=BO(B在Y轴正半轴上),
∵点A坐标为(1,1),O为坐标原点,
∴OA=OB=
 ,
,∴B1=(0,
 ),
),②当AO=BO(B在Y轴负半轴上),
同理:B2=(0,-
 ).
).③当AO=BO(B在X轴正半轴上),
同理:B3=(
 ,0).
,0).④当AO=BO(B在X轴负半轴上),
同理:B4=(-
 ,0).
,0).(2)当AO,AB为腰时,
⑤当AO=BO(B在Y轴正半轴上),
∵点A坐标为(1,1),O为坐标原点,
∴B5=(0,2).
⑥当AO=BO(B在X轴正半轴上),
同理:B6=(2,0).
(3)当AO为底时,
⑦AB=BO(B在Y轴正半轴上),
同理:B7=(0,1).
⑧当AB=BO(B在X轴正半轴上),
同理:B8=(1,0).
故选C.
点评:此题主要考查等腰三角形的性质及坐标与图形性质的综合运用,注意分类讨论思想的运用.

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 <0),作PC⊥PB交过点A的直线l于点C(4,y).
<0),作PC⊥PB交过点A的直线l于点C(4,y).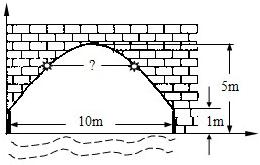 如图是某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯.若把拱桥的截面图放在平面直角坐标系中,则两盏景观灯之间的水平距离是( )
如图是某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯.若把拱桥的截面图放在平面直角坐标系中,则两盏景观灯之间的水平距离是( )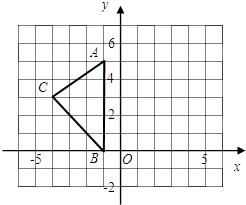 21、如图,在平面直角坐标系中,A(-1,5)、B(-1,0)、C(-4,3).
21、如图,在平面直角坐标系中,A(-1,5)、B(-1,0)、C(-4,3).