题目内容
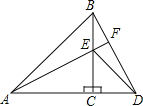
【题目】如图1，
，
平分
，以
为顶点作
，交
于点
，
于点E.
（1）求证：
；
（2）图1中，若
，求
的长；
（3）如图2，
，平分，以为顶点作
，交于点，于点
.若，求四边形
的面积.
【答案】（1）见解析；（2）OD+OE =
；（3）
【解析】
（1）过点C作CG⊥OA于G,CH⊥OB于H，然后根据题意利用AAS定理进行证明△CDG ≌ △CEH，从而求解；
（2）根据全等三角形的性质得到OD+OE =2OH，然后利用勾股定理求OH的值，从而求解；
（3）过点C作CG⊥OA于G,CH⊥OB于H，然后根据题意利用AAS定理进行证明△CDG ≌ △CEH，从而求得
=
=2
，然后利用含30°的直角三角形性质求得OH=
,CH=
从而求得三角形面积，使问题得到解决.
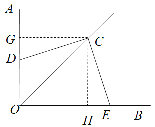
解：（1）如图,过点C作CG⊥OA于G,CH⊥OB于H，
∵
平分
∴CG =CH
∵
,
∴∠CDO+∠CEO=180
∵∠CDG+∠CDO=180
∴∠CDG =∠CEO
在△CDG与△CEH中
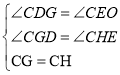
∴△CDG ≌ △CEH(AAS)
∴
(2)由（1）得△CDG ≌ △CEH
∴DG=HE
由题易得△OCG与△OCH是全等的等腰直角三角形，且OG=OH
∴OD+OE=OD+OH+HE=OG+OH=2OH
设OH=CH=x，在Rt△OCH中，由勾股定理，得:
OH2+CH2=OC2
∴
∴
(舍负)
∴OH =
∴OD+OE =2OH=
（3）如图,过点C作CG⊥OA于G,CH⊥OB于H，
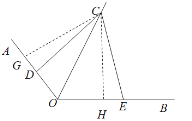
∵平分
∴CG =CH
∵
,
∴∠CDO+∠CEO=180
∵∠CDG+∠CDO=180
∴∠CDG =∠CEO
在△CDG与△CEH中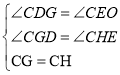
∴△CDG ≌ △CEH(AAS)
∴DG=HE
由题易得△OCG与△OCH是全等的直角三角形,且OG=OH
∴OD+OE=OD+OH+HE=OG+OH=2OH
∴==2
在Rt△OCH中,有∠COH=60°,OC=3，
∴OH=,CH=
∴
∴=2=
