题目内容
在直角坐标系xOy中，已知A（-2，1），B（2，3），则x轴上存在一点C，使A到C与B到C的距离和最小．则C点的坐标是
- A.（-2，0）
- B.（-1，0）
- C.（0，0）
- D.（1，0）
B
分析：根据题意画出图形，先求出点A关于x轴的对称点A′的坐标，连接A′B，利用待定系数法求出直线A′B的解析式，求出此直线与x的交点即为C点坐标．
解答：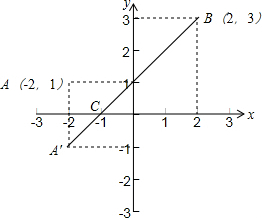
解：如图所示：
作点A关于x轴的对称点A，′连接A′B，
∵A（-2，1），
∴A′（-2，-1），
设直线A′B的解析式为y=kx+b（k≠0），
∵B（2，3），
∴
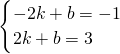，解得
，
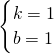∴此直线的解析式为y=x+1，
∴当y=0时，x=-1，
∴C（-1，0）．
故选B．
点评：本题考查的是轴对称-最短路线问题，熟知“两点之间，线段最短”是解答此题的关键．
分析：根据题意画出图形，先求出点A关于x轴的对称点A′的坐标，连接A′B，利用待定系数法求出直线A′B的解析式，求出此直线与x的交点即为C点坐标．
解答：
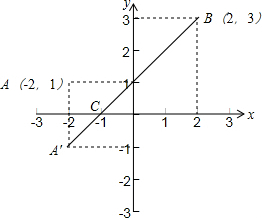解：如图所示：作点A关于x轴的对称点A，′连接A′B，
∵A（-2，1），
∴A′（-2，-1），
设直线A′B的解析式为y=kx+b（k≠0），
∵B（2，3），
∴
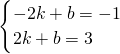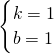，解得，∴此直线的解析式为y=x+1，
∴当y=0时，x=-1，
∴C（-1，0）．
故选B．
点评：本题考查的是轴对称-最短路线问题，熟知“两点之间，线段最短”是解答此题的关键．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
在直角坐标系xoy中，函数y=4x的图象与反比例函数y=
（2012•北京二模）已知：如图，在直角坐标系xOy中，点A（8，0）、B（0，6），点C在x轴的负半轴上，AB=AC．动点M在x轴上从点C向点A移动，动点N在线段AB上从点A向点B移动，点M、N同时出发，且移动的速度都为每秒1个单位，移动时间为t秒（0＜t＜10）．
析式为y=x2-mx+n．方程x2-mx+n=0的两根倒数和为-4．