题目内容
点D、E分别是线段AC与BC的中点，BE=8cm，AC=5cm，求DE．
解：∵点D、E分别是线段AC与BC的中点，
∴AC=2DE，CE=BE，
∵CD=2.5cm，CE=8cm，
∴DE=CE+DC=8+2.5=10.5cm．
分析：由中点的性质可知，AC=2DE，CE=BE，再由BE=8cm，AC=5cm，即可求出CD=2.5cm，CE=8cm，然后如图DE=CE+DC，即可推出结果．
点评：本题主要考查线段中点的性质，两点间的距离，关键在于根据题意推出CD=2.5cm，CE=8cm．
∴AC=2DE，CE=BE，
∵CD=2.5cm，CE=8cm，
∴DE=CE+DC=8+2.5=10.5cm．
分析：由中点的性质可知，AC=2DE，CE=BE，再由BE=8cm，AC=5cm，即可求出CD=2.5cm，CE=8cm，然后如图DE=CE+DC，即可推出结果．
点评：本题主要考查线段中点的性质，两点间的距离，关键在于根据题意推出CD=2.5cm，CE=8cm．
练习册系列答案
名校课堂系列答案
相关题目
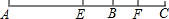
在实数m，使得△APQ与△AEC相似？如存在，请求出实数m的值；如不存在，请说明理由．
如图，点E，F分别是线段AC，BC的中点，若EF=3厘米，则线段AB=