题目内容
20.把多项式$\frac{3}{2}$x2+$\frac{5}{3}$-3x+$\frac{1}{2}$x3按字母x的降幂排列为:$\frac{1}{2}$x3+$\frac{3}{2}$x2-3x+$\frac{5}{3}$.分析 先分清各项,然后按降幂排列的定义解答.
解答 解:把多项式$\frac{3}{2}$x2+$\frac{5}{3}$-3x+$\frac{1}{2}$x3按字母x的降幂排列为:$\frac{1}{2}$x3+$\frac{3}{2}$x2-3x+$\frac{5}{3}$.
故答案为:$\frac{1}{2}$x3+$\frac{3}{2}$x2-3x+$\frac{5}{3}$.
点评 此题主要考查了多项式幂的排列.我们把一个多项式的各项按照某个字母的指数从大到小或从小到大的顺序排列,称为按这个字母的降幂或升幂排列.
要注意,在排列多项式各项时,要保持其原有的符号.

练习册系列答案
相关题目
12.已知A、B、C都是直线l上的点,且AB=5cm,BC=3cm,则AC=( )
| A. | 8cm | B. | 2cm | C. | 4cm | D. | 8cm或者2cm |
9.不等式-3x+6<0的正整数解有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 无数多个 |
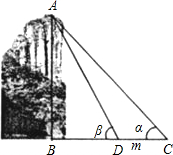 如图,为测得峰顶A到河面B的高度h,当游船行至C处时测得峰顶A的仰角为α,前进m米至D处时测得峰顶A的仰角为β(此时C、D、B三点在同一直线上).当α=44°,β=61°,m=50米时,求h的值.(精确到1米)
如图,为测得峰顶A到河面B的高度h,当游船行至C处时测得峰顶A的仰角为α,前进m米至D处时测得峰顶A的仰角为β(此时C、D、B三点在同一直线上).当α=44°,β=61°,m=50米时,求h的值.(精确到1米)