Question

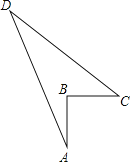
【题目】如图，一块形如四边形ABCD的草地中，AB＝3m，BC＝4m，CD＝12m，DA＝13m，且∠ABC＝90°，要以AC、CD、DA为边制作围栏，问围栏长多少米，草地面积多大？

Answer 1

【答案】24m2．

【解析】

连接AC，利用勾股定理求出AC，再根据勾股定理的逆定理证得△DAC是直角三角形，且∠DAC是直角，再根据四边形ABCD的面积为=S△DAC﹣S△ABC计算即可得到答案.

连接AC，

∵∠ABC＝90°，AB＝4m，BC＝3m，

∴AC＝5m，

∵CD＝13m，AD＝12m，

∴AC2+AD2＝CD2，

∴△DAC是直角三角形，且∠DAC是直角，

∴S△DAC＝×AD×AC＝×12×5＝30（m2），

∴四边形ABCD的面积为：S△DAC﹣S△ABC＝30﹣×3×4＝24（m2）．