题目内容
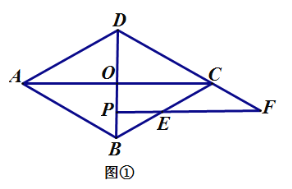
【题目】已知菱形![]() 的对角线交于点
的对角线交于点![]() 是直线
是直线![]() 上任意一点(异于点
上任意一点(异于点![]() ),过点
),过点![]() 作平行于
作平行于![]() 的直线交直线
的直线交直线![]() 于点
于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
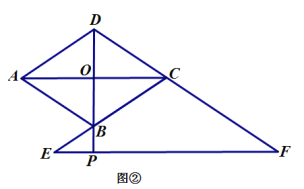
(1)当点![]() 在线段
在线段![]() 上时,如图 ①,易证:
上时,如图 ①,易证:![]() (不用证明);
(不用证明);
(2)当点![]() 在线段
在线段![]() 的延长线上时,如图 ②;当点
的延长线上时,如图 ②;当点![]() 在线段
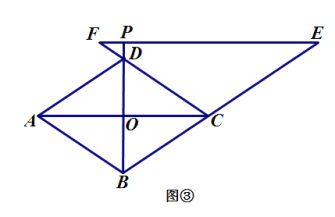
在线段![]() 的延长线上时,如图 ③,线段
的延长线上时,如图 ③,线段![]() 之间又有怎样的数量关系? 请写出你的猜想,并选择其中一种情况加以证明.
之间又有怎样的数量关系? 请写出你的猜想,并选择其中一种情况加以证明.
【答案】(1)证明详见解析;(2)图②的结论为![]() ;图③的结论为
;图③的结论为![]() ;详见解析.
;详见解析.
【解析】
(1)先解直角三角形AOB得出AO=![]() ,由菱形的性质得到AC=
,由菱形的性质得到AC=![]() ,延长FP交AB于点G,证明四边形AGFD是平行四边形得到AC=FG,再证明PE=PG即可得到答案;
,延长FP交AB于点G,证明四边形AGFD是平行四边形得到AC=FG,再证明PE=PG即可得到答案;
(2)在②中延长FE交BC的延长线于G,可证得PF=PG,再证明四边形ACGE为平行四边形可得AC=EG,可证得![]() ;在③中,延长CB交EF于点G,可证明PG=PF,可得到
;在③中,延长CB交EF于点G,可证明PG=PF,可得到![]()
(1)∵四边形ABCD是菱形,∠DAB=60°,
∴∠OAB=30°,∠AOB=90°,![]() ,
,![]()
∴![]()
∴![]()
∴![]()
延长FP交AB于点G,

∵AB//CD,AC//FG
∴四边形ACFG是平行四边形,
∴AC=FG(平行四边形的对边相等)
∵EG//AC,
∴![]() (被平行线所截的线段对应成比例)
(被平行线所截的线段对应成比例)
又∵OA=OC
∴PE=PG,
∴AC=FG=PF+PG=PE+PF
∴![]()
![]() )当P在DB的延长线上时,如图②,结论为
)当P在DB的延长线上时,如图②,结论为![]()
证明:延长FE交DA的延长线于点G,

∵AC∥FG,
∴![]() ,
,
∵四边形ABCD为菱形,
∴AO=CO,
∴PF=PG,
∴EG=PG-PE=PF-PE,
又∵AB∥CG,AC∥EG,
∴四边形ACEG为平行四边形,
∴AC=EG,
∴AC=PF-PE,
![]()
当P在BD的延长线上时,如图③,结论为![]()
延长EF交BA的延长线于点G,
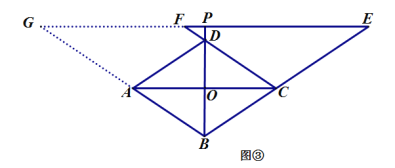
∵AC∥EF,
∴![]() ,
,
∵四边形ABCD为菱形,
∴AO=CO,
∴PG=PE,
∴FG=PG-PF=PE-PF,
又∵AC∥EG,AG∥CF,
∴四边形AGFC为平行四边形,
∴FG=AC,
∴AC=PE-PF,
∴![]() .
.

 巧学巧练系列答案
巧学巧练系列答案