题目内容
【题目】如图，四边形ABCO为矩形，点A在x轴上，点C在y轴上，且点B的坐标为（－1，2），将此矩形绕点O顺时针旋转90°得矩形DEFO，抛物线y=－x2+bx+c过B，E两点．
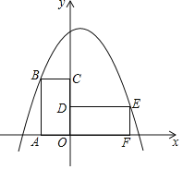
（1）求此抛物线的函数关系式；
（2）将矩形ABCO向上平移，并且使此抛物线平分线段BC，求平移距离．
【答案】（1）
；（2）
.
【解析】
（1）用待定系数法即可解决问题．
（2）设平移的距离为h，BC的中点为M，得出M的坐标，代入抛物线的解析式，求解即可．
（1）由题意，点E的坐标为（2，1），则
，解得：
，∴此抛物线的解析式为．
（2）设平移的距离为h，平移后BC的中点为M，则C（0，2+h），B（－1，2+h），M（
，2+h）．
∵M在抛物线上，∴
，解得：h=．
答：平移距离为．
练习册系列答案
相关题目
