题目内容
如图,E、F分别是矩形ABCD的边AD、BC上的点,且AE=CF.求证:四边形EBFD为平行四边形.
【答案】分析:由题意易得ED∥BF,AD=BC而AE=CF,那么可得到ED=BF,即可求证.
解答:(本小题满分9分)
证明:∵ABCD为矩形,
∴AD∥BC且AD=BC.(2分)
又∵AE=CF,
∴AD-AE=BC-CF,(4分)
即ED=BF,(6分)
由ED∥BF且ED=BF,(8分)
得四边形EBFD为平行四边形.(9分)
(一组对边平行且相等的四边形为平行四边形).
点评:本题综合应用了平行四边形的性质和判定,要根据条件合理、灵活地选择方法.
解答:(本小题满分9分)
证明:∵ABCD为矩形,
∴AD∥BC且AD=BC.(2分)
又∵AE=CF,
∴AD-AE=BC-CF,(4分)
即ED=BF,(6分)
由ED∥BF且ED=BF,(8分)
得四边形EBFD为平行四边形.(9分)
(一组对边平行且相等的四边形为平行四边形).
点评:本题综合应用了平行四边形的性质和判定,要根据条件合理、灵活地选择方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

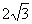 ,直线y=
,直线y=
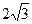 ,直线y=
,直线y=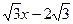 经过点C,交y轴于点G
经过点C,交y轴于点G
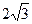 ,直线y=
,直线y=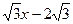 经过点C,交y轴于点G
经过点C,交y轴于点G
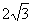 ,直线y=
,直线y=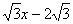 经过点C,交y轴于点G
经过点C,交y轴于点G