题目内容
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() .(1)已知点
.(1)已知点![]() 在第一象限的抛物线上,则点
在第一象限的抛物线上,则点![]() 的坐标是_______.(2)在(l)的条件下连接
的坐标是_______.(2)在(l)的条件下连接![]() ,
,![]() 为抛物线上一点且
为抛物线上一点且![]()
![]() ,则点
,则点![]() 的坐标是_______.
的坐标是_______.

【答案】(1) ![]() (2)
(2) ![]()
【解析】
(1)由题意把![]() 点坐标
点坐标![]() 代入函数解析式求出m,并由
代入函数解析式求出m,并由![]() 点在第一象限判断点
点在第一象限判断点![]() 的坐标;
的坐标;
(2)利用相似三角形相关性质判定![]() ≌
≌![]() ,并根据题意设
,并根据题意设![]() ,则
,则![]() ,表示P,把
,表示P,把![]() 代入函数解析式从而得解.
代入函数解析式从而得解.
解:(1)把![]() 点坐标
点坐标![]() 代入函数解析式
代入函数解析式![]() 得
得![]()
解得![]()
∵![]() 点在第一象限
点在第一象限
∴![]()
∴![]()
∴![]()
(2)∵![]() (
(![]() 作为特殊角,处理方法是作其补角
作为特殊角,处理方法是作其补角![]() )
)
∴过点![]() 作
作![]() 延长线于点
延长线于点![]()
∵![]() ,
,![]()
∴![]() 为等腰直角三角形
为等腰直角三角形
∴![]() (因为
(因为![]() ,
,![]() ,所以考虑构造一线三垂直,水平竖直作垂线)
,所以考虑构造一线三垂直,水平竖直作垂线)
∴过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() 于点
于点![]()
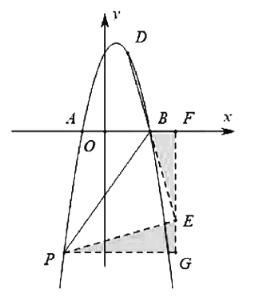
∴![]() ≌
≌![]()
∵![]()
∴![]()
∴![]()
设:![]() ,则
,则![]()
∴![]()
∴![]() (注意咱们设
(注意咱们设![]() ,
,![]() 为整数,
为整数,![]() 点在第三象限,横纵坐标为负数,所以
点在第三象限,横纵坐标为负数,所以![]() 点的坐标表示要注意正负!)
点的坐标表示要注意正负!)
把![]() 代入函数解析式得
代入函数解析式得![]()
解得![]() 或6(
或6(![]() 舍去)
舍去)
∴![]()
∴![]() .
.

练习册系列答案
相关题目