题目内容
11.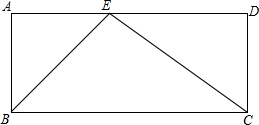 如图,在矩形ABCD中,BE平分∠ABC交AD于E,AB=1,CE=2,求∠BEC的度数及BE,BC的长.
如图,在矩形ABCD中,BE平分∠ABC交AD于E,AB=1,CE=2,求∠BEC的度数及BE,BC的长.
分析 先求出∠ABE=∠AEB=45°,得出AE=AB=1,即可求出∠BEC;再根据勾股定理求出DE,即可求出AD,即为BC.
解答 解:∵四边形ABCD是矩形,
∴∠A=∠ABC=∠D=90°,CD=AB=1,BC=AD,
∵BE平分∠ABC,
∴∠ABE=45°,
∴∠AEB=45°,
∴AE=AB=1,
∴BE=$\sqrt{A{B}^{2}+A{E}^{2}}$=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
又∵CE=2,
∴CD=$\frac{1}{2}$CE,
∴∠CED=30°,DE=$\sqrt{3}$CD=$\sqrt{3}$,
∴∠BEC=180°-45°-30°=105°,AD=AE+DE=1+$\sqrt{3}$,
∴BC=1+$\sqrt{3}$.
点评 本题考查了矩形的性质、等腰直角三角形的判定与性质以及勾股定理的运用;志明三角形是等腰直角三角形和运用勾股定理是解题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
1.已知4个数据:-$\sqrt{2}$、2$\sqrt{2}$、a、b,其中a、b是方程x2-2x-1=0的两个根,则这4个数据的中位数是( )
| A. | 0.5 | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
 如图,若三个小正方形的边长都为2,则图中阴影部分面积的和是$\frac{3π}{2}$.
如图,若三个小正方形的边长都为2,则图中阴影部分面积的和是$\frac{3π}{2}$.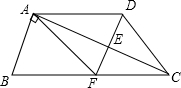 已知:如图,在梯形ABCD中,AD∥BC,BC=2AD,AC⊥AB,点E是AC的中点,DE的延长线与BC相交于点F.求证:四边形AFCD是菱形.
已知:如图,在梯形ABCD中,AD∥BC,BC=2AD,AC⊥AB,点E是AC的中点,DE的延长线与BC相交于点F.求证:四边形AFCD是菱形.