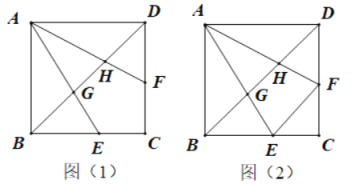
题目内容
【题目】如图，在矩形
中，
是
的中点，动点
在线段
上，连接
并延长交射线
于点
，过点
作
的垂线交
于点
，设
的中点为
，连接
，
．
(1)当点不与点
重合时，求证：
；
（2）①当点与点或点
重合时，
是等腰直角三角形，当点与点或点不重合时，请判定的形状；
②求点移动的最长距离．
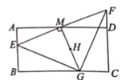
【答案】（1）详见解析；（2）①等腰直角三角形，理由详见解析；②
．
【解析】
（1）由矩形的性质可以得出∠A=∠FDM=90°，∠AEM=∠DFM，再证明AM=DM即可证出结论；
（2）①如图1，过点
作
于
，证
，推出
，再证GF=GE，即可判定
的形状；
②由题意可判断出点H的运动路程为CG的一半，可直接写出结果；
(1)∵四边形
是矩形，
∴
，
是
的中点，
，
又
，
；
（2）①过点作于，如图①，
，
是矩形，
，
，
，
，
，
，
，
∵
是的中点，
，
，
，
，
，
由（1）得
，
，
，
，
，
是等腰直角三角形；
②如图②，当点
与点
重合时，
，
，
为
的中点，
当点运动到
时，点与
重合，
，
，
∴点
移动的最长距离为．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
