题目内容
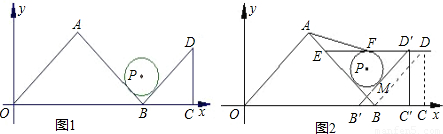
(2003•仙桃)如图1,在x轴正半轴上以OB为斜边、BC为直角边向第一象限分别作等腰Rt△AOB和Rt△CDB. OA=8,BC=4,在∠ABD内有一半径为1,且与AB、BD相切的⊙P.(1)写出⊙P的圆心坐标;
(2)若△CDB在x轴上以每秒2个单位的速度向左匀速平移,⊙P同时相应在BA和BD上滑动,且保持与BA、BD相切,至⊙P终止运动.设运动时间为t秒,试用含t的代数式表示P点坐标;并证明P点的横、纵坐标之和为定值;
(3)如图2,过D点作x轴的平行线交AB于E,D’B’与AB交于M,在满足(2)的前提下,t取何值时,⊙P可成为△D’EM的内切圆;如果⊙P与DE相切于点F,求△AEF的面积.
【答案】分析:(1)根据等腰直角三角形的性质可求,点P的横坐标和纵坐标;
(2)由等腰直角三角形BBM的性质可知:设点P的横坐标为8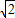 -t,把P点的纵横坐标用t表示出来,从而找出P点的横、纵坐标之间的关系.
-t,把P点的纵横坐标用t表示出来,从而找出P点的横、纵坐标之间的关系.
(3)当⊙P成为△D′EM的内切圆时,根据内切圆的性质,分别求出D′M,B′M,D′M,BB′,再根据已知关系求出t值,从而求出三角形AEF的面积.
解答:解:

(1)作PM⊥AB,
∵圆P与AB、BD与P相切,
∴BP平分∠ABD,
∵∠ABO=∠DBC,
∴∠ABD=90°,
∴∠PBA=45°,
∴∠ABO+∠PBA=90°,即BP⊥x轴,
而BP=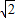 r=
r=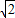 ,OB=
,OB=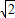 OA=8
OA=8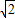 ,
,
∴点P的横坐标为8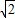 ,纵坐标为
,纵坐标为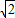 ,则P(8
,则P(8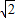 ,
,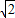 ),
),
(2)根据题意可知,点P的横坐标为8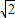 -t,纵坐标为
-t,纵坐标为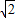 +t,则P(8
+t,则P(8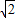 -t,
-t, +t),
+t),
因为8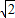 -t+
-t+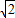 +t=9
+t=9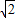 ,所以P点的横、纵坐标之和为定值;
,所以P点的横、纵坐标之和为定值;
(3)当⊙P成为△D′EM的内切圆时,D′M=2+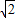 ,B′M=4
,B′M=4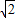 -D′M=3
-D′M=3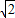 -2,BB′=6-2
-2,BB′=6-2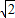 ,
,
即2t=6-2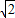 ,得t=3-
,得t=3-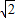 ,
,
S△AEF= ×(
×(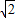 +1)(4
+1)(4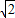 -
-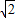 -1-3+
-1-3+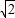 )=2.
)=2.
点评:此题是一个动点问题,考查正方形的性质,中位线的性质及图形面积的求法,作为压轴题,综合了初中阶段的重点知识,能够培养同学们综合运用知识的能力.
(2)由等腰直角三角形BBM的性质可知:设点P的横坐标为8
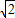 -t,把P点的纵横坐标用t表示出来,从而找出P点的横、纵坐标之间的关系.
-t,把P点的纵横坐标用t表示出来,从而找出P点的横、纵坐标之间的关系.(3)当⊙P成为△D′EM的内切圆时,根据内切圆的性质,分别求出D′M,B′M,D′M,BB′,再根据已知关系求出t值,从而求出三角形AEF的面积.
解答:解:

(1)作PM⊥AB,
∵圆P与AB、BD与P相切,
∴BP平分∠ABD,
∵∠ABO=∠DBC,
∴∠ABD=90°,
∴∠PBA=45°,
∴∠ABO+∠PBA=90°,即BP⊥x轴,
而BP=
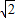 r=
r=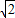 ,OB=
,OB=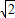 OA=8
OA=8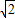 ,
,∴点P的横坐标为8
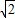 ,纵坐标为
,纵坐标为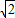 ,则P(8
,则P(8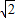 ,
,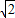 ),
),(2)根据题意可知,点P的横坐标为8
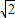 -t,纵坐标为
-t,纵坐标为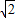 +t,则P(8
+t,则P(8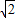 -t,
-t, +t),
+t),因为8
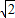 -t+
-t+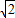 +t=9
+t=9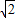 ,所以P点的横、纵坐标之和为定值;
,所以P点的横、纵坐标之和为定值;(3)当⊙P成为△D′EM的内切圆时,D′M=2+
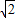 ,B′M=4
,B′M=4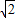 -D′M=3
-D′M=3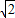 -2,BB′=6-2
-2,BB′=6-2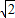 ,
,即2t=6-2
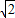 ,得t=3-
,得t=3-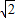 ,
,S△AEF=
 ×(
×(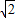 +1)(4
+1)(4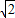 -
-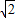 -1-3+
-1-3+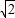 )=2.
)=2.点评:此题是一个动点问题,考查正方形的性质,中位线的性质及图形面积的求法,作为压轴题,综合了初中阶段的重点知识,能够培养同学们综合运用知识的能力.

练习册系列答案
相关题目
 .
. ,OE=
,OE=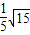 ,求AD:DF的值;
,求AD:DF的值;



