题目内容
1. 如图,AB是⊙O的直径,点F为圆上一点,AE平分∠BAF交⊙O于点E,过点E作直线与AF垂直,交AF的延长线于点D,交AB的延长线于点C
如图,AB是⊙O的直径,点F为圆上一点,AE平分∠BAF交⊙O于点E,过点E作直线与AF垂直,交AF的延长线于点D,交AB的延长线于点C(1)试证明CD与⊙O相切于点E.
(2)若BC=2,AD=3,求⊙O的半径及∠AED的度数.
分析 (1)要证CD是⊙O的切线,只要连接OE,再证∠OED=90°即可.
(2)设⊙O的半径为x,由OE∥AD,得出比例式$\frac{OE}{AD}=\frac{OC}{AC}$,求出半径,得出∠OCE=30°,由直角三角形的性质得出∠CAD=60°,求出∠CAE=∠DAE=30°,即可得出∠AED的度数.
解答 (1)证明:连接OE,如图所示: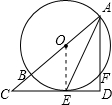
∵AE平分∠BAF,
∴∠CAE=∠DAE.
∵OA=OE,
∴∠OEA=∠CAE.
∴∠DAE=∠OEA.
∴OE∥AD,
∵AD⊥CD,
∴OE⊥CD,
∴CD与⊙O相切于点E;
(2)解:设⊙O的半径为x,
由(1)得:OE∥AD,
∴$\frac{OE}{AD}=\frac{OC}{AC}$,即$\frac{x}{3}=\frac{x+2}{2x+2}$,
解得:x=2,或x=-1.5(不合题意,舍去),
∴⊙O的半径为2,
在Rt△OCE中,OE=2,OC=2+2=4,
∴OC=2OE,
∴∠OCE=30°,
∴∠CAD=90°-30°=60°,
∴∠CAE=∠DAE=30°,
∴∠AED=90°-30°=60°.
点评 本题考查了切线的判定、等腰三角形的性质、平行线的判定与性质、平行线分线段成比例定理等知识;本题综合性强,有一定难度,运用平行线分线段成比例定理求出半径是解决问题的关键.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
12.把二次函数y=x2-4x+1化成y=a(x+m)2+k的形式是( )
| A. | y=(x-2)2+1 | B. | y=(x-2)2-1 | C. | y=(x-2)2+3 | D. | y=(x-2)2-3 |
9.方程x(x+2)=0的解是( )
| A. | -2 | B. | 0,-2 | C. | 0,2 | D. | 无实数根 |
16.一元二次方程x2+kx-3=0的一个根是x=1,则另一个根是( )
| A. | -3 | B. | -1 | C. | 2 | D. | 3 |
13.下列事件中是必然事件的是( )
| A. | 实心铁球投入水中会沉入水底 | B. | 某投篮高手投篮一次就投中 | ||
| C. | 打开电视机,正在播放足球比赛 | D. | 抛掷一枚硬币,落地后正面朝上 |
11.解方程$\frac{x}{3}-\frac{x-1}{2}=1$时,去分母后,正确的是( )
| A. | 3x-2(x-1)=1 | B. | 2x-3(x-1)=1 | C. | 3x-2(x-1)=6 | D. | 2x-3(x-1)=6 |