题目内容
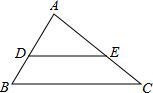如图，已知D、E在△ABC的边上，DE∥BC，∠B=60°，∠AED=45°，则∠A的度数为
- A.65°
- B.75°
- C.85°
- D.95°
B
分析：根据平行线的性质可得∠C=∠AED=45°，再利用三角形内角和为180°可以计算出∠A的度数．
解答：∵DE∥BC，
∴∠C=∠AED=45°，
∴∠A=180°-∠B-∠C=180°-45°-60°=75°，
故选：B．
点评：此题主要考查了三角形内角和定理，关键是掌握三角形内角和为180°．
分析：根据平行线的性质可得∠C=∠AED=45°，再利用三角形内角和为180°可以计算出∠A的度数．
解答：∵DE∥BC，
∴∠C=∠AED=45°，
∴∠A=180°-∠B-∠C=180°-45°-60°=75°，
故选：B．
点评：此题主要考查了三角形内角和定理，关键是掌握三角形内角和为180°．
练习册系列答案
相关题目
7、如图，已知D、E分别在AB、AC上，且AE=AD，AC=AB，CD与BE交于点O，DB=EC则图中的全等三角形有（ ）
如图，已知∠AOM=60°，在射线OM上有点B，使得AB与OB的长度都是整数，由此称B是“完美点”，若OA=8，则图中完美点B的个数为（ ）
如图，已知ABC三点在圆O上，连接ABCO，如果∠AOC=140°，则∠B的度数为
如图，已知C、D分别在OA、OB上，并且OA=OB，OC=OD，AD和BC相交于E，则图中全等三角形的对数是（ ）