题目内容
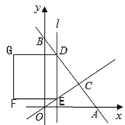
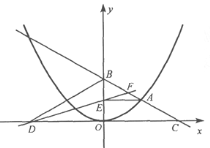
【题目】如图,在平面直角坐标系中,A是抛物线![]() 上的一个动点,且点A在第一象限内.AE⊥y轴于点E,点B坐标为(0,2),直线AB交
上的一个动点,且点A在第一象限内.AE⊥y轴于点E,点B坐标为(0,2),直线AB交![]() 轴于点C,点D与点C关于y轴对称,直线DE与AB相交于点F,连结BD.设线段AE的长为m,△BED的面积为S.
轴于点C,点D与点C关于y轴对称,直线DE与AB相交于点F,连结BD.设线段AE的长为m,△BED的面积为S.
(1)当![]() 时,求S的值.
时,求S的值.
(2)求S关于![]() 的函数解析式.
的函数解析式.
(3)①若S=![]() 时,求
时,求![]() 的值;
的值;
②当m>2时,设![]() ,猜想k与m的数量关系并证明.
,猜想k与m的数量关系并证明.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)①
;(3)①![]() ;②
;②![]() ,证明见解析.
,证明见解析.
【解析】
试题分析:(1)根据点在曲线上点的坐标与方程的关系,求出点A的坐标,根据△ABE∽△CBO求出CO的长,从而根据轴对称的性质求出DO的长,进而求出△BED的面积S.
(2)分![]() 和
和![]() 两种情况讨论.
两种情况讨论.
(3)①连接AD,由△BED的面积为![]() 求出
求出![]() 现,得到点A 的坐标,应用待定系数法,设
现,得到点A 的坐标,应用待定系数法,设![]()
![]() 得到
得到![]() ,从而
,从而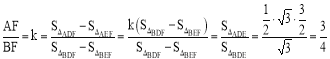 .
.
②连接AD,应用待定系数法,设![]() 得到
得到![]() ,从而得到
,从而得到![]() ,因此
,因此 .
.
![]() 得到
得到![]() ,从而
,从而
试题解析:(1)∵点A是抛物线![]() 上的一个动点,AE⊥y轴于点E,且
上的一个动点,AE⊥y轴于点E,且![]() ,
,
∴点A的坐标为![]() .∴当
.∴当![]() 时,点A的坐标为
时,点A的坐标为![]() .
.
∵点B的坐标为![]() ,∴BE=OE=1.
,∴BE=OE=1.
∵AE⊥y轴,∴AE∥x轴. ∴△ABE∽△CBO.∴![]() ,即
,即![]() ,解得
,解得![]() .
.
∵点D与点C关于y轴对称,∴![]() .
.
∴![]() .
.
(2)①当![]() 时,如图,
时,如图,
∵点D与点C关于y轴对称,∴△DBO≌△CBO.
∵△ABE∽△CBO,∴△ABE∽△DBO .∴![]() .∴
.∴![]()
∴![]() .
.

②当![]() 时,如图,同①可得
时,如图,同①可得![]()

综上所述,S关于![]() 的函数解析式
的函数解析式![]() .
.
(3)①如图,连接AD,
∵△BED的面积为![]() ,∴
,∴![]() .∴点A 的坐标为
.∴点A 的坐标为![]() .
.
设![]() ,∴
,∴![]() .
.
∴![]() .
.
∴ .
.

②k与m的数量关系为![]() ,证明如下:
,证明如下:
连接AD,则
∵![]() ,∴
,∴![]() .
.
∴![]() .
.
∵点A 的坐标为![]() ,∴
,∴ .
.


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目