题目内容
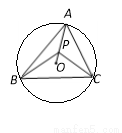
如图,⊙O的直径AB和弦CD相交于点E,已知AE=1cm,EB=5cm,∠DEB=600,求弦CD的长。
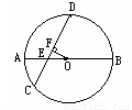
2 cm.
cm.
【解析】
试题分析:作OF⊥CD于F,连接OD,求出AB=6cm,半径OD=3cm,在Rt△OFE中,OE=2cm,∠OEF=60°,由勾股定理求出OF= cm,在Rt△OFD中,由勾股定理得求出FD=
cm,在Rt△OFD中,由勾股定理得求出FD= cm,由垂径定理得出DC=2DF,代入即可;
cm,由垂径定理得出DC=2DF,代入即可;
试题解析:作OF⊥CD于F,连接OD,

∵AE=1cm,BE=5cm,E在直径AB上,
∴AB=1cm+5cm=6cm,半径OD=3cm,
∵在Rt△OFE中,OE=3cm-1cm=2cm,∠OEF=60°,
∴OF= cm,
cm,
在Rt△OFD中,由勾股定理得:FD= cm,
cm,
∵OF⊥CD,
∴由垂径定理得:DC=2DF=2 cm.
cm.
考点:1.垂径定理;2.勾股定理.

练习册系列答案
相关题目