题目内容
3.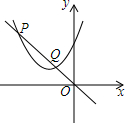 如图,一次函数y1=-x与二次函数y=ax2+bx+c的图象相交于P,Q两点,则函数y=ax2+(b+1)x+c的图象可能为( )
如图,一次函数y1=-x与二次函数y=ax2+bx+c的图象相交于P,Q两点,则函数y=ax2+(b+1)x+c的图象可能为( )| A. | 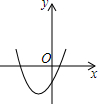 | B. | 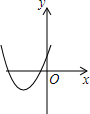 | C. |  | D. | 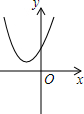 |
分析 由一次函数y1=-x与二次函数y2=ax2+bx+c图象相交于P、Q两点,得出方程ax2+(b+1)x+c=0有两个不相等的根,进而得出函数y=ax2+(b+1)x+c与x轴有两个交点,根据方程根与系数的关系得出函数y=ax2+(b+1)x+c的对称轴x=-$\frac{b+1}{2a}$<0,即可进行判断.
解答 解:∵一次函数y1=-x与二次函数y2=ax2+bx+c图象相交于P、Q两点,
∴方程ax2+(b+1)x+c=0有两个不相等的根,
∴函数y=ax2+(b+1)x+c与x轴有两个交点,
∵-$\frac{b}{2a}$<0,a>0
∴-$\frac{b+1}{2a}$=-$\frac{b}{2a}$-$\frac{1}{2a}$<0
∴函数y=ax2+(b-1)x+c的对称轴x=-$\frac{b+1}{2a}$<0,
∵a>0,开口向上,
故选:B.
点评 本题考查了二次函数的图象,直线和抛物线的交点,交点坐标和方程的关系以及方程和二次函数的关系等,熟练掌握二次函数的性质是解题的关键.

练习册系列答案
相关题目
15.在1,2,3,4,5中,能使得代数式(x-1)(x-2)(x+3)(x+4)的值为零的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
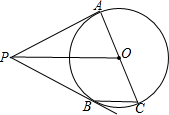 如图,已知P为⊙O外一点,PA、PB为⊙O的切线,切点为A、B,AC是直径.
如图,已知P为⊙O外一点,PA、PB为⊙O的切线,切点为A、B,AC是直径. 如图是数值转换机示意图,各步应填入的转换步骤:第一步为:平方,第二步为:-2,第三步为:×3.
如图是数值转换机示意图,各步应填入的转换步骤:第一步为:平方,第二步为:-2,第三步为:×3. 如图所示,某学校拟建一个含内接矩形的菱形花坛(花坛为轴对称图形),矩形的四个顶点分别在菱形四条边上,菱形ABCD的边长AB=4 m,∠ABC=60°.设AE=x m(0<x<4),矩形EFGH的面积为Sm2.求:
如图所示,某学校拟建一个含内接矩形的菱形花坛(花坛为轴对称图形),矩形的四个顶点分别在菱形四条边上,菱形ABCD的边长AB=4 m,∠ABC=60°.设AE=x m(0<x<4),矩形EFGH的面积为Sm2.求: