题目内容
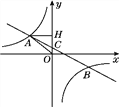
【题目】如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=![]() (k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=
(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=![]() ,点B的坐标为(m,-2).
,点B的坐标为(m,-2).
(1)求△AHO的周长;
(2)求该反比例函数和一次函数的解析式.
【答案】(1)△AHO的周长为12;(2) 反比例函数的解析式为y=![]() ,一次函数的解析式为y=-
,一次函数的解析式为y=-![]() x+1.
x+1.
【解析】试题分析: (1)根据正切函数,可得AH的长,根据勾股定理,可得AO的长,根据三角形的周长,可得答案;
(2)根据待定系数法,可得函数解析式.
试题解析:(1)由OH=3,tan∠AOH=![]() ,得
,得
AH=4.即A(-4,3).
由勾股定理,得
AO=![]() =5,
=5,
△AHO的周长=AO+AH+OH=3+4+5=12;
(2)将A点坐标代入y=![]() (k≠0),得
(k≠0),得
k=-4×3=-12,
反比例函数的解析式为y=![]() ;
;
当y=-2时,-2=![]() ,解得x=6,即B(6,-2).
,解得x=6,即B(6,-2).
将A、B点坐标代入y=ax+b,得
![]() ,
,
解得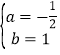 ,
,
一次函数的解析式为y=-![]() x+1.
x+1.
考点:反比例函数与一次函数的交点问题.
【题型】解答题
【结束】
21
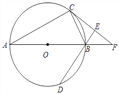
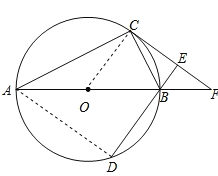
【题目】如图,AB为⊙O的直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,过点C作CE⊥DB交DB的延长线于点E,直线AB与CE相交于点F.
(1)求证:CF为⊙O的切线;
(2)填空:当∠CAB的度数为________时,四边形ACFD是菱形.
【答案】30°
【解析】(1)连结OC,如图,由于∠A=∠OCA,则根据三角形外角性质得∠BOC=2∠A,而∠ABD=2∠BAC,所以∠ABD=∠BOC,根据平行线的判定得到OC∥BD,再CE⊥BD得到OC⊥CE,然后根据切线的判定定理得CF为⊙O的切线;
(2)根据三角形的内角和得到∠F=30°,根据等腰三角形的性质得到AC=CF,连接AD,根据平行线的性质得到∠DAF=∠F=30°,根据全等三角形的性质得到AD=AC,由菱形的判定定理即可得到结论.
答:
(1)证明:连结OC,如图,
∵OA=OC,
∴∠A=∠OCA,
∴∠BOC=∠A+∠OCA=2∠A,
∵∠ABD=2∠BAC,
∴∠ABD=∠BOC,
∴OC∥BD,
∵CE⊥BD,
∴OC⊥CE,
∴CF为⊙O的切线;
(2)当∠CAB的度数为30°时,四边形ACFD是菱形,理由如下:
∵∠A=30°,
∴∠COF=60°,
∴∠F=30°,
∴∠A=∠F,
∴AC=CF,
连接AD,
∵AB是⊙O的直径,
∴AD⊥BD,
∴AD∥CF,
∴∠DAF=∠F=30°,
在△ACB与△ADB中,
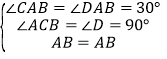 ,
,
∴△ACB≌△ADB,
∴AD=AC,
∴AD=CF,
∵AD∥CF,
∴四边形ACFD是菱形。
故答案为:30°.

 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案