题目内容
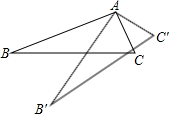 如图,在Rt△ABC中,∠BAC=90°,AB=12,BC=13.将其绕着它的顶点A逆时针旋转25°至△AB′C′的位置,则AC′=
如图,在Rt△ABC中,∠BAC=90°,AB=12,BC=13.将其绕着它的顶点A逆时针旋转25°至△AB′C′的位置,则AC′=考点:旋转的性质
专题:计算题
分析:先根据勾股定理计算出AC=5,然后根据旋转的性质求解.
解答:解:∵∠BAC=90°,AB=12,BC=13,
∴AC=-
-=5,
∵△ABC绕着它的顶点A逆时针旋转25°至△AB′C′的位置,
∴AC′=AC=5,∠CAC′=25°.
故答案为:5,25°.
∴AC=-
| BC2-AB2 |
∵△ABC绕着它的顶点A逆时针旋转25°至△AB′C′的位置,
∴AC′=AC=5,∠CAC′=25°.
故答案为:5,25°.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了勾股定理.

练习册系列答案
相关题目
下列函数中,是反比例函数的是( )
A、y=-
| ||
B、y=
| ||
| C、y=2x-1 | ||
D、y=
|
下列语句正确的是( )
| A、延长线段AB到C,使BC=AC |
| B、反向延长线段AB,得到射线BA |
| C、取直线AB的中点 |
| D、连接A、B两点,并使直线AB经过C点 |
 如图,在菱形ABCD中,∠A=135°,AB=
如图,在菱形ABCD中,∠A=135°,AB=
 矩形OABC在直角坐标系中的位置如图所示,A、C两点的坐标分别为A(6,0)、C(O,3),直线y=
矩形OABC在直角坐标系中的位置如图所示,A、C两点的坐标分别为A(6,0)、C(O,3),直线y= 如图,已知大正方形和小正方形的边长分别为a、b
如图,已知大正方形和小正方形的边长分别为a、b