题目内容
2.定义:如果两个函数的交点横坐标至少有一个在指定范围内,我们就称这两个函数在这个范围内是互为友好函数.(1)若函数y=2x+m-1与函数y=x+1在0<x<2上是友好函数,求m的取值范围;
(2)若函数y=2x+m-1与函数y=-$\frac{1}{x}$在0<x<2上是友好函数,求m的取值范围;
(3)若函数y=2x+m-1过点(0,1),且与函数y=x2+x+c在0≤x≤2上是友好函数,求c的取值范围.
分析 (1)(2)两个函数联立方程,求得方程的解,得出m的取值范围;
(3)把点(0,1)代入y=2x+m-1,求得m,再把x=0,或x=2代入y=2x+m-1求得y,代入y=x2+x+c得出c的取值范围.
解答 解:(1)由题意得,
2x+m-1=x+1,
解得x=-m-2,
∵0<-m-2<2,
∴-4<m<-2;
(2)由题意得2x+m-1=-$\frac{1}{x}$
2x2+(m-1)x+1=0,
△=(m-1)2-4×2×1=0,
解得:m=1+2$\sqrt{2}$,或m=1-2$\sqrt{2}$,
当m=1+2$\sqrt{2}$时,解得x=-$\frac{\sqrt{2}}{2}$,不合题意,
当m=1-2$\sqrt{2}$时,解得x=$\frac{\sqrt{2}}{2}$,符合题意,
因此x=1-2$\sqrt{2}$;
(3)∵把点(0,1)代入y=2x+m-1,得m=2,
∴y=2x+1,
∴$\left\{\begin{array}{l}{y=2x+1}\\{y={x}^{2}+x+c}\end{array}\right.$,消去y得:x2-x+c-1=0,
∵△≥0
∴c≤$\frac{5}{4}$,
由题意知,x2-x+c-1=0的正数解在0与2之间,
即0≤$\frac{1+\sqrt{5-4c}}{2}$≤2,
解得:-1≤c≤$\frac{5}{4}$.
点评 此题考查一次函数、反比例函数、二次函数的性质,理解有好函数的意义,建立方程解决问题.

练习册系列答案
相关题目
10.如图1所示,E、F分别为透明正方体的面ADD1A1,面BCC1B1的中心,则四边形BFD1E的正视图、左视图、俯视图分别是图2中的( )
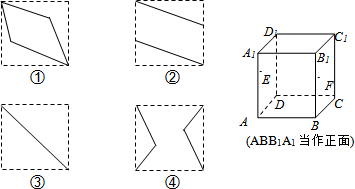

| A. | ②③② | B. | ①②① | C. | ①②③ | D. | ②③④ |
17.a,b互为相反数,下列各数中,互为相反数的一组为( )
| A. | a2与b2 | B. | a3与b5 | ||
| C. | a2n与b2n (n为正整数) | D. | a2n+1与b2n+1 |
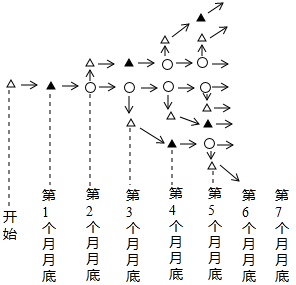 如果用△表示一对新出生的小兔,用▲表示一对一个月大的成年兔子,用○表示一对能生小兔的成年兔子,请你在图中标出第6个月月底和第7个月月底的各对兔子,把这幅图补充完整.
如果用△表示一对新出生的小兔,用▲表示一对一个月大的成年兔子,用○表示一对能生小兔的成年兔子,请你在图中标出第6个月月底和第7个月月底的各对兔子,把这幅图补充完整.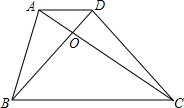 已知:在梯形ABCD中,AD∥BC.
已知:在梯形ABCD中,AD∥BC.