题目内容
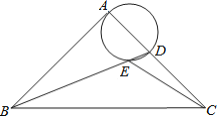
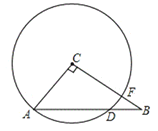
【题目】如图，△ABC中，∠C=90°，AC=6,BC=8,以点C为圆心，CA的长为半径的圆与AB、BC分别相交于点D、F，求圆心到AB的距离及AD的长．
【答案】(1)圆心到AB的距离为4.8;(2) AD=3.6.
【解析】
首先过点C作CE⊥AD于点E，由∠ACB=90°，AC=6，BC=8，可求得AB的长，又由直角三角形斜边上的高等于两直角边乘积除以斜边，即可求得CE的长，由勾股定理求得AE的长，然后由垂径定理求得AD的长．
过点C作CE⊥AD于点E，则AE=DE，∵∠ACB=90°，AC=6，BC=8，∴AB=
=10，∵S△ABC=
ACBC=ABCE，∴CE=
=
=4.8，∴AE=
=1.8，∴AD=2AE=3.6．
练习册系列答案
相关题目
